The universal set is a set that contains elements of all the related sets, without repeating the elements with itself. Let say if X and Y are two sets, such as X = {1,3} and Y = {1,a,c}, then the universal set associated with these two sets is given by U = {1,3,a,c}.
Universal Set Definition -:
A set that contains all the elements of other sets, along with its own elements is known as a universal set It is usually denoted by the symbol ‘U’.
- Let say , set P consists of all even numbers such that, P = {2, 4, 6, 8, 10, …} and set Q consists of all odd numbers, such that, Q = {1, 3, 5, 7, 9, …}. The universal set U consists of all-natural numbers, such that, U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10,….}. Therefore, as very well known, all the even and odd numbers are a part of natural numbers. Therefore, the universal set has all the elements of Set P and Q.
Complement of Universal Set –
There is a complement of the set for every set. The complement of the universal set is an empty set. This means where the Universal set consists of a set of all elements, the empty set contains no elements of the subsets. The empty set will also be called a Null set. It is denoted by ‘{}’.
Examples of the universal set –
If a universal set will be infinite, or even if it’s finite with many numbers of elements, then the ellipses, the three dots (…), are used to represent the universal set. An example is given below :
U = {1, 2, 3, …}
Or, U = {1, 2, 3, …, 4000}
Let’s solve some examples to develop a firm understanding of universal sets -:
Example 1 -:
Consider, that there are three sets, namely A, B, and C. The elements in each set are given by-
A={2, 4, 6}
B={3, 7, 8,}
C={4, 8, 10}
Calculate the universal set for sets A, B, and C?
Solution -: As the universal set consists of all the elements without repetition of the given sets; thus, the universal set of A, B, and C is given by:
U={2, 3, 4, 6, 7, 8, 10}
Example 2 –: Let P is equal to a set of odd numbers, and Q is equal to the set of even numbers. Can you tell the universal set of P and Q?
Solution –: The sets P and Q can be written as:
P = {1, 3, 9…} and,
Q = {2, 4, 6,…}
So, the universal set is:
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10…}
From the above example, we observe that the universal set U of the sets P and Q results in the set of natural numbers.
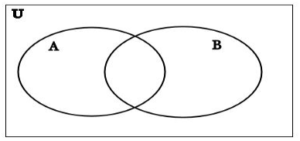
Representation of Universal Set through Venn Diagram -:
- The Venn Diagram represents two or more circles used to demonstrate the relationships among different sets of finite elements or objects.
- In the Venn diagram, the circles are used to demonstrate sets. These circles or sets are contained within the universal set, which is represented by a rectangle.
Properties of Universal Set-:
The following properties of universal sets are discussed here-:
If U is the universal set and X, Y and Z are any 3 finite sets then;
- If X and Y are any two finite sets then n(X – Y) = n(X) – n(X ∩ Y) i.e. n(X – Y) + n(X ∩ Y) = n(X).
- If X and Y are any two finite units then n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y)
- If X and Y are any finite units then n(X ∪ Y) = n(X) + n(Y) ⇔ X, Y are disjoint non-void sets.
- If X and Y are any two finite sets then n(X ∪ Y) = a variety of elements that belongs to exactly certainly one of X or Y.
n((X – Y) ∪ (Y – X))
= (X – Y) + n(Y – X) [Since (X – Y) and (Y – X) are disjoint.]
= n(X) – n(X ∩ Y) + n(Y) – n(X ∩ Y)
= n(X) + n(Y) – 2n(X ∩ Y)
5. X ∪ X’ = U
For Example: If U = {1 , 2 , 3 , 4 , 5 } and X = {1 , 2 , 3 } then X’ = {4 , 5}. From this it can be seen that-:
X ∪ X’ = U = { 1 , 2 , 3 , 4 , 5}
6. Law of empty set and universal set: As per this law the complement of the universal set gives us the empty set and vice-versa i.e.,
∅’ = U And U’ = ∅
Conclusion –
The universal set is denoted by U and is a set that contains all the elements of all its subsets, including its own elements, and the elements are not repeated. Here, we have discussed the universal set, complement of the set, empty set and properties of the universal set. We have discussed how to represent the universal set through a Venn diagram. The concept of set has been discussed in an explanatory way and quoted with examples to understand the concept in a better way.