We conduct operations in mathematics such as addition, subtraction, multiplication, and so on. These operators usually take two or more operands and return a result based on the operation. In set theory, some operations are typically done on two or more sets to produce a new set of items based on the operation. The amount of elements carried by the operation and executing the result of a collective set are represented by the union and intersection of sets. In the case of a union, all elements are considered, whereas in the case of an intersection, just the common elements are taken into account.
Union of Sets
When two or more sets are combined, a completely new set is created that contains components from both sets. The word ‘or’ is used to represent the union of sets. Consider the two sets A and B. All of the elements that are present in either A or B, or both sets, will be present in the union of A and B. The union of sets is represented by the set operation.:
A ∪ B = {x: x ∈ A or x ∈ B}. Here, x is an element which is present in both the two sets, A and B.
Finding a Union of Sets
To further understand how to find the union of sets, consider the following example. As A = a, b, j, k and B = h, t, k, c, we have two sets A and B. The elements present in the union of A and B must be identified.
The resultant set will comprise elements that are present in A, B, or both sets, according to the definition of the union of two sets. As a result, the elements of both sets are a, b, c, j, k, h, and t. However, because the element k appears in both sets, it will be considered only once. a, b, c, j, k, h, t are the elements contained in the union of sets A and B.
Notation of Union of Set
The union of two sets is represented by the mathematical symbol “. The operands are encircled by this operator, which is termed infix notation.
Consider two sets P and Q, then Union Is P ∪ Q.
Venn diagram of Union of Sets
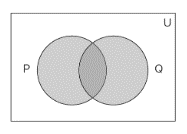
In the above-given Venn diagram, the blue-coloured region shows the union of sets P and Q. This further represents that the union between these sets includes all the elements that are present in P or Q or both sets. Although the union operation between two sets was utilised in this example, the Venn diagram is frequently used to depict the union of several sets, as long as the sets are finite.
Conclusion
When two sets are combined, a whole new set is created that contains all of the components from both sets. All components that are present in the first set, the second set, or both sets are included in the resultant set. Use the formula to find the cardinal number of the union of sets:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B).