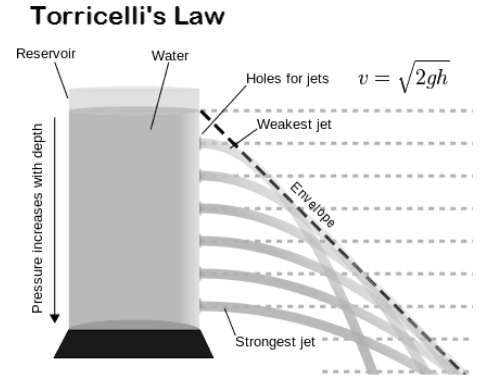
Torricelli’s theorem, also known as Torricelli’s law, Torricelli’s principle, or Torricelli’s equation, states that the speed, v, of a liquid flowing under gravity out of an opening in a tank is proportional to the square root of the vertical distance, h, between the liquid surface and the centre of the opening and the square root of twice the acceleration caused by gravity, simply v=(2gh)1/2. (At the Earth’s surface, gravity causes an acceleration of around 32.2 feet per second per second, or 9.8 metre per second per second.) Evangelista Torricelli, who discovered the theorem in 1643, is named for him.
Torricelli’s Law
Torricelli’s law, also called Torricelli’s principle or Torricelli’s theorem, is a fluid dynamics statement that specifies the efflux velocity from orifice.
According to Torricelli’s law, the speed at which fluid flows from an orifice is equal to the speed It would descend freely for a distance equal to the free surface height of the liquid above the aperture.
Consider any vessel having a slit (orifice) filled with liquid.
The fluid will begin to flow through the slit, and according to Torricelli’s law, the speed with which the fluid will flow is equal to the speed with which a freely falling body reaches a height equal to the height of the slit from the fluid’s free surface.
The distance between the free surface and the slit should be equal to h.
The velocity with which the fluid flows is identical to the velocity attained by a freely falling body falling from a height of h.

Torricelli’s law, also known as Torricelli’s principle or Torricelli’s theorem, is a statement in fluid dynamics that the speed, v, of fluid flowing out of an orifice in a tank under gravity is proportional to the square root of the vertical distance, h, between the liquid surface and the centre of the orifice, and to the square root of twice the acceleration caused by gravity.
In other words, the fluid’s efflux velocity from the orifice is the same as it would have been if it had fallen h feet under gravity. Evangelista Torricelli, an Italian scientist, discovered the law in 1643 and named it after him. Later, it was discovered to be a special case of Bernoulli’s principle.
p1+1 / 2pv1²+pgh1=p2+1 / 2pv2²+pgh2
For a certain circumstance, Torricelli’s equation is derived. Viscosity and other losses must be ignored, and the orifice must be tiny. In Bernoulli’s Equation, if a fluid is flowing through a very small orifice (for example, at the bottom of a big tank), the velocity of the fluid at the large end can be ignored. Furthermore, efflux velocity is unaffected by flow direction. The efflux speed of fluid passing through the opening is thus given by the formula:
v= √2gh
Use of Torricelli’s law
Torricelli’s law is useful in everyday situations. The physical law describes a significant link between liquid exit velocity and container height. This post will teach you about this relationship and how to use Torricelli’s theorem to calculate exit velocity.
Applications
Horizontal distance covered by the jet of liquid
The horizontal distance traversed by the jet of liquid to reach the same level as the base of the liquid column can be simply calculated if display style HH is the height of the orifice above the ground and display style HH is the height of the liquid column from the ground (height of liquid’s surface). We have from the rules of falling bodies that display style HH is the vertical height travelled by a particle of jet stream.
h=1 / 2gt²=>t= √2h / g ,
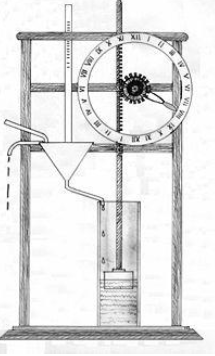
Clepsydra problem
A clepsydra is a clock that uses the movement of water to measure time. It is made up of a pot with a little hole at the bottom that allows the water to escape. The amount of water that escapes determines the length of time. According to Torricelli’s law, the rate of efflux via the hole is proportional to the water level, and the discharge is not uniform as the water level drops. Keeping the water level steady is a simple method. This can be accomplished by allowing a continual stream of water to flow into the vessel, with the overflow being permitted to exit via another hole at the top.

An inflow clepsydra
As a result of the consistent height, the discharging water from the bottom can be collected in a second cylindrical vessel with a uniform graduation for time measurement. This is a clepsydra with inflow.
Alternatively, the water level in the vessel can be controlled to decline at a moderate pace by carefully selecting the vessel’s design. The time can be measured with uniform graduation by monitoring the level of water remaining in the vessel.
Conclusion
Torricelli’s theorem, also known as Torricelli’s law, Torricelli’s principle, or Torricelli’s equation, states that the speed, v, of a liquid flowing under gravity out of a tank opening is proportionate to the square root of the vertical distance, h, between the liquid surface and the centre…