
In this article, we will discuss the important concept of Mensuration. Mensuration is a branch of mathematics that deals with lengths of lines, surface area, and volume of solid figures. Figures such as square, rectangle, trapezium, and triangle lie entirely in the plane. These figures are known as plane figures and are in 2-dimensional form. The perimeter and area can be measured from these plane figures. However, we come across 3-dimensional objects such as cube, cuboid, sphere, cylinder, and cones in our everyday life. These figures are called solid figures. These figures possess surface area and volume. Hence, in this article, we will explore the surface area and volume with examples.
Surface area and volume
The rectangle is a plane figure with four sides. The sum of all lengths of four sides is called the perimeter of the rectangle. The area is nothing but the region enclosed by the plane or solid. Similarly, the sum of all the three sides of the triangle is called the perimeter of the triangle and the area is the region enclosed in it.
The surface area and volume can be measured in solid figures like cubes and cuboids. The surface area is the measurement of the surface constituting the solid. The volume of the solid figure measures the space region enclosed by the solid figure.
Units of surface area and volume
The unit of the surface area is similar to the area of plane figures. The surface area is measured in square units. The volume is measured in cubic units. When the unit cube of 1 cm is chosen, the unit for volume is cm3. Similarly, when the unit cube of 1 m is chosen, the unit for volume is m3 and so on.
Cuboids
Surface area of the cuboid
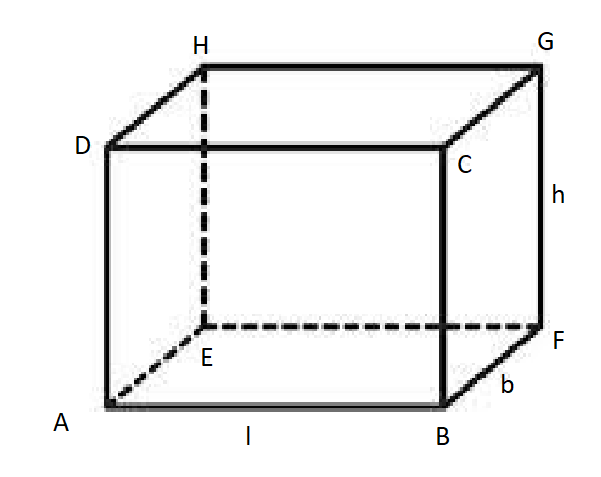
The primary examples of cuboids include brick, match box, and chalk box. In this diagram, we can see the cuboid’s length, breadth, and height. Let the vertices be ABCDEFGH with six rectangular faces.

We already know that the surface area of the solid figure is the measurement of the sum of the areas of all the six faces.
Here, the surface can be calculated as
(l x b) + (b x h) + (h x l) + (l x b) + (b x h) + (h x l)
= 2( lb + bh + hl)
Now, draw the line joining BE and EC,
BE2 = AB2 + AE2
(As ∠EAB = 900)
Or BE2 = l2 + b2 —-(1)
Also, EC2 = BC2 + BE2
(As ∠CBE = 900)
Or EC2 = h2 + l2 + b2
Hence, EC = √ h2 + l2 + b2
Hence , diagonal of a cuboid = √ h2 + l2 + b2
Volume of cuboid
The volume of the cuboid is equal to the product of the length, breadth, and height.
Volume = length x breadth x height
Volume of the cuboid V = lbh
Cubes
Surface area of the cube
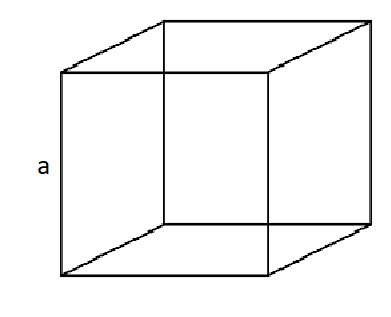
The cube is a particular type of cuboid in which all the parameters such as length, breadth, and height are equal.

In the above figure, we can see six equal faces of the cube.
The surface area of a cube can be given by
2 ( a x a + a x a + a x a)
= 6a2
The diagonal of the cube = √ a2 + a2 + a2 = a √ 3
Volume of the cube
The volume of the cube of side a is given by
V = a x a x a = a3
Cones
Surface area of the cone
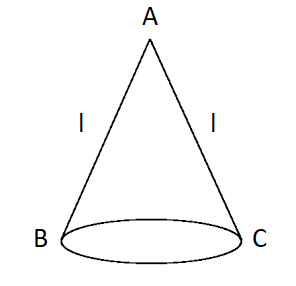
Let us consider a hollow right circular cone with radius r and height h. Let the sector of a circle of radius l and its arc length is equal to 2r.

Area of this sector = Arc length/Circumference
= 2πr . πl2/2πl
Then, curved surface of the cone = area of the sector
= πrl
The surface area of the cone = πrl + πr2
= πr ( l +r)
Volume of the cone
Let us take two solid figures, a right-angled cone and right-angled cylinder of same base radius and height. The volume of the cone with radius r and height h is one-third the volume of the cylinder.
Thus, the volume of the cone = ⅓ volume of the cylinder
= ⅓ πr2h
Cylinders
Surface area of cylinder


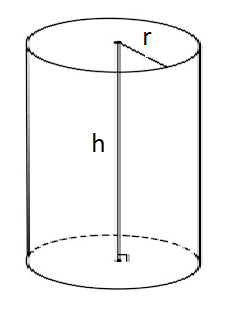
Let us consider a hollow cylinder of radius r and height h . When we cut it along any line, we obtain a rectangle of length 2r and breadth h. The area of the rectangle is equal to the area of the curved surface of the cylinder.
Curved surface area of the cylinder = area of rectangle
= 2πr x h
= 2πrh
When both the ends of the cylinder are closed, then the total surface area of the cylinder
= 2πrh + 2πr2
= 2πr ( r+h)
Volume of the cylinder
The volume of the cylinder = area of the base x height
V = πr2 x h
V = πr2h
Conclusion
In this article, we have briefly discussed the surface area and volume of solid figures in detail. Mensuration is essential for engineers to do projects and understand the solid objects in 3-dimensional space, helping them create or make models and solve various problems mathematically in several scenarios. Volume and surface area are the two parameters that easily measure a 3D solid object. In this surface area and volume study material, we have discussed solid figures such as cube, cuboid, cone, and cylinder with their formulas.