The topic of height and distance in physics holds tremendous importance. This topic is significant in competitive examinations. You can understand it better with the help of solved problems on height and distance. The problems of this topic usually revolve around the measurement of a building’s height. They could also involve finding the height of another building when one building’s height and angles of elevation or depression are shown. Another form could be finding the distance between these two buildings. Keep on reading to benefit from such solved problems on height and distance.
Solved Problems on Height and Distance: Associated Terms
Before we delve into solved problems on height and distance, you must first become familiar with some associated terms:
Angle of Elevation: Suppose an individual is standing on the ground. This individual’s sight is on an object at the top of a building. Here, the line of sight would be the line that joins the individual’s eyes with the building’s top. Most importantly, the elevation angle would be the angle produced by the line of sight with the horizontal line.
The angle of Depression: Suppose an individual is standing at some height of an object that can be viewed. Here, the line of sight would be the line that joins the individual’s eyes with the building’s bottom. Most importantly, the angle of depression would be the angle produced by the line of sight with the horizontal line.
These terms would become clearer to you by studying solved problems on height and distance.
Solved Problems on Height and Distance: Examples:
Let’s look at the solved problems on height and distance examples below:
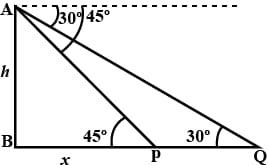
1. From a lighthouse’s top that is 80m high, someone observes two ships. The angles of elevation of these ships that are observed from this lighthouse’s top come out to be 45° and 30°, respectively. Now, measure the distance between the two ships that are being observed?
Solution:

Here, let us consider AB or h is 80 m, which is the lighthouse.
Moreover, consider the ships to be at points P and Q.
In ΔBAP, tan 45° = BA/BP
As such, 1 = 80/BP
Therefore, BP or x = 80m
Therefore, BQ = 80 + PQ
In ΔBAQ, tan30° = BA/BQ
As such, 1/√3 = 80/(80+PQ)
Furthermore, (80+PQ) = 80√3
Finally, we have PQ = 80(√3-1) = 80 x 0.732 = 58.56m
Therefore, the distance between the ships as observed from the lighthouse’s top is 58.56m.
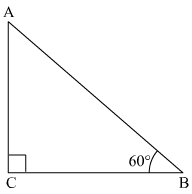
2. The angle of elevation of the building’s top is found to be 60°. This building is located at a distance of 50 m when measured from its foot on a horizontal plane. Now, calculate the building’s height?

Here, the building’s height is represented by AC.
Moreover, BC shows us the distance between the building and the point of observation.
Now, consider the right triangle ACB:
Here, side AC is the side that lies opposite to the angle of elevation, ∠60°.
Also, the hypotenuse side AB is the side that lies opposite to 90°. Furthermore, the adjacent side BC is the remaining side.
Now, given the above parameters, we need to calculate the length of the side AB.
Tanθ = opposite side/adjacent side. This gives us tan60° = AC/BC
Furthermore, √3 = AC/50
Also, √3 x 50 = AB
AC = 50√3
Approximate value of √3 comes out to be 1.732
So, we have AC = 50 (1.732)
Finally, we have AC = 86.6 m
So, the building’s height comes out to be 86.6 m.
Solved Problems on Height and Distance Questions
Let’s take a look at the solved problems on height and distance questions below:
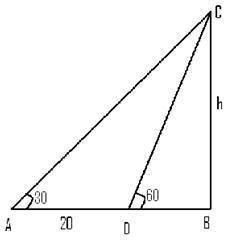
1. On level ground, a 30° angle of elevation is formed with the top of a tower. Now, on moving towards the tower by 20 metres, a 45° angle of elevation would form. What is the tower’s height out of the four options?
– 10√3
– √3
– 10
– 20√3
Correct Answer: A
Explanation:

Consider the height of the tower to be h
In such a situation, we have 20 = h (cot30 – cot60)
Furthermore, 20 = h (√3 – 1/√3)
Also, 20√3 = h (3-1)
Finally, we have h = 10√3
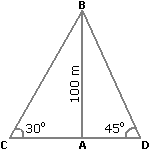
2. There are two ships that are sailing on the two sides of a particular lighthouse. The angles of elevation, as observed from the ships and from the top of the lighthouse, are 30° and 45°, respectively. Now, suppose the height of the lighthouse is 100 m. What is the distance between the two ships out of the four options given below?
A. 173 m
B. 200 m
C. 300 m
D. 273 m
Correct Answer: D
Explanation:
|
|---|
Consider the lighthouse to be represented by AB.
Also, let us assume the ships positions to be C and D.
In such a situation, we shall have the following:
AB = 100 m
∠ACB = 30°
∠ADB = 45°
AB/AC = tan 30° = 1/√3
This would give us AC = AB x √3 = 100/√3
Now, we will have
AB/AD = tan 45° = 1
This would give us
AD = AB = 100m
Therefore, we have CD = AC + AD
So, AC + AD = 100/√3 + 100m
Finally, we have, CD = 273 m.
Conclusion
The topic of height and distance is an important constituent of physics. Study any Physics chapter, and there are chances that you would be dealing with height and distance in some way or another. The solved problems on height and distance are a must for mastering this topic. The angle of elevation and the angle of depression are two associated terms with this topic. Finally, study the solved problems on height and distance examples and questions for a thorough understanding.