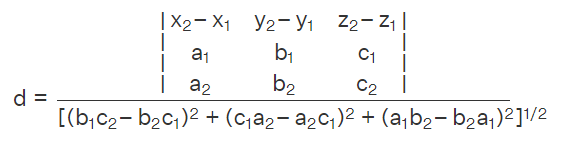
Skew lines can be defined as the pair of parallel lines that do not meet. Skew lines can only exist in spaces with more than two dimensions. They must be non-coplanar, which means that they exist in distinct planes. Two lines in a two-dimensional space can cross or be parallel to each other. As a result, skew lines don’t define in 2D space.
Skew lines may be encountered in a variety of scenarios in real life. Assume there is a line on the ceiling and a line on the wall. These lines can be skew lines if they are not parallel to each other and do not meet because they reside in distinct planes. These lines are endlessly long in both directions.
We must first understand three different sorts of lines before learning about skew lines. The following are the details:
- Intersecting Lines – Intersecting lines are two or more lines that cross each other at a certain location and reside in the same plane.
- Parallel Lines – Parallel lines are two or more lines that never intersect even when stretched endlessly and are in the same plane.
- Coplanar Lines- Lines that are coplanar lie in the same plane.
Definition of Skew Lines
Skew lines are non-intersecting, non-parallel, and non-coplanar pairs of lines. This means that skew lines will never meet and will never be parallel. In order for lines to exist on two dimensions or in the same plane, they must intersect or be parallel. Skew lines are non-coplanar and exist in three or more dimensions because this property does not apply to them.
Example of Skew Lines
Different kind of roadways, for example, motorways and overpasses etc., can be found in a city in real life. This roadway can be thought to be on separate planes. Lines created on such roadways never connect and are never parallel to one another, resulting they are skew lines.
Skew Lines in 3 Dimension
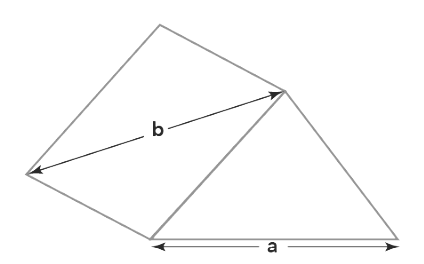
Skew lines will always exist in 3D space since they are non-coplanar by definition. Assume we have the following three-dimensional solid form. On the triangular face, we draw one line and call it ‘a.’ On the quadrilateral-shaped face, we draw one line and label it ‘b.’ Neither a nor b are enclosed on the same plane. If we stretch ‘a’ and ‘b’ in both directions indefinitely, they will never intersect and will not be parallel to each other. Thus, in 3D, skew lines ‘a’ and ‘b’ are instances. Slight deviations in parallel or intersecting lines in 3D space will almost always result in skew lines.

Distance Between the Two given Lines
The distance between two lines can be termed as the distance between the two lines. A line is a figure made by connecting two points with a minimal distance between them and extending both ends of the line to infinity. The perpendicular distance between two lines can be used to compute the distance between them. The distance between two parallel lines is usually calculated.
In addition, the shortest distance between two non-intersecting lines in the same plane is the distance that is the smallest of all the distances between two points on both lines.
The shortest distance between two skew lines
Let us first define skew lines before looking for the formula to compute the shortest distance between them. Skew lines are seen in the multidimensional system when two lines are not parallel but never meet. Only in three dimensions or more is this conceivable.
Let’s look at how to get the shortest distance between two skew lines whose equations are: –
r1 = a1+tb1and r2 = a2+tb2 is:
d=|(a2−a1).(b1×b2)”https://unacademy.com/”(b1×b2)|
If the lines’ equations are written in cartesian form, the distance between them is:
(x–x1)/a1 = (y–y1)/b1 = (z–z1)/c1
(x–x2)/a2 = (y–y2)/b2 = (z–z2)/c2
Is
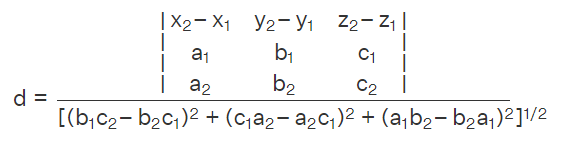
Important Information About Skew Lines
Skew lines are lines that are not intersecting, parallel, or coplanar.
Skew lines can only defined in 3 D or more. As a result, skew lines are not possible in 2D space.
The shortest distance between skew lines may be calculated using both vector and cartesian forms of the formula.
Conclusion
Skew lines are two lines that do not meet and are not parallel in three dimensions. A pair of skew lines are lines that cross-opposing edges of a regular tetrahedron. Skew lines are only defined in three or more dimensions as two lines in the same plane that must either cross each other or will be parallel to one another. A pair of skew lines is usually always defined by four random locations within a unit cube.