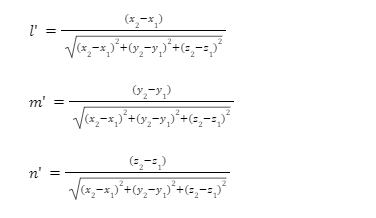
In mathematical terms, the word “projection” means “The representation of a figure or solid on a plane as it would look from a particular direction.” There are several types of projections in terms of line segments and points. The two specific types are the projection of a point on a line and the projection of a line segment joining two points on a line. Here the point or the line may or may not belong to the parent line.
Projecting a line segment joining two points on a line is equivalent to calculating the length of the original line segment as projected on the new line.
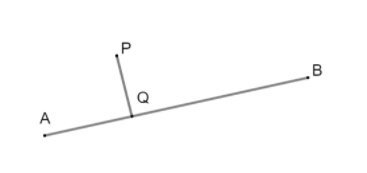
Consider a point P and AB be the given line. Draw a perpendicular from the point P as on AB and mark that point as Q. This point Q is called the projection of point P on line AB.

Types of projection of a line segment
- Projection of a point on a line
The projection of a point on a line can be further sub-categorised into two parts: The point not belonging to the line and the point belonging to the line.
Not belonging to the line
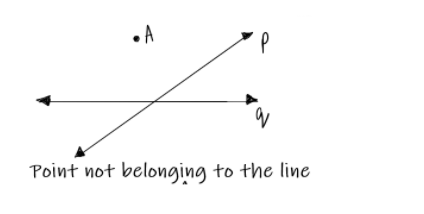
Here, point A does not belong to both p and q.

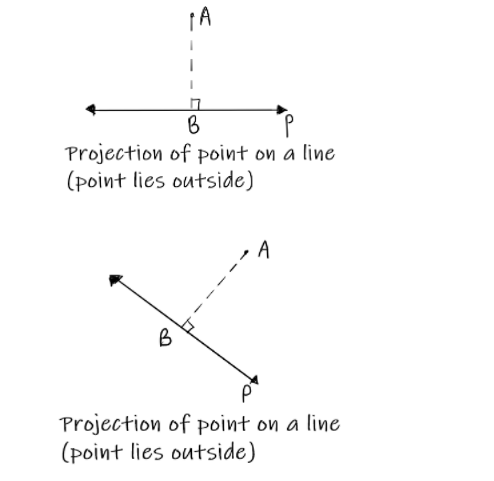
- The projection of a point on a line when it is external to the line, i.e. a point not belonging to the line, is “A point that represents the foot of the perpendicular drawn from the point to the line”. An example of this is shown below:

Here, point A is projected on line P at point B. Therefore, B behaves as the foot of the perpendicular.
Belonging to the line
The second case is where the point belongs to the line.
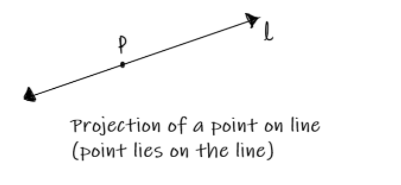
The projection of a point on a line when it is on the line, i.e., a point belonging to the line, is “the point itself”. It is shown below:

Here point P lies on line l; therefore, its projection is point P itself.
Now let us consider the second case:
Projection of a line segment joining two points on a line
The projection of a line segment joining two points on a line is the line segment, formed by taking the projection of the endpoints of the parent line segment on the existing line. Here also, we have two cases where one of the points on the line segment lies on the line and the other where none of the points on the line segment lies on the line. Let us observe both cases:
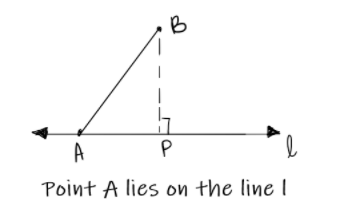
When one end of the line segment lies on the line

Here one endpoint of the line segment AB is lying on line l. The projection of B on line l is “P,” and that of point A on line l is “A” itself.
Therefore, the projection of AB on l will be equivalent to finding the length of “AP”.
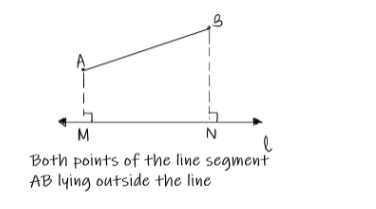
When both the points of the line segment do not fall on the given line

Here AB is the line segment and l is a line, where both points A and B don’t lie on line l. The projection of point A on l is M, and that of point B is N.
Therefore, the projection of line AB on l will be equivalent to finding the length of “MN”.
Let us understand the projection of the line segment joining two points on a line in detail to understand the formula.
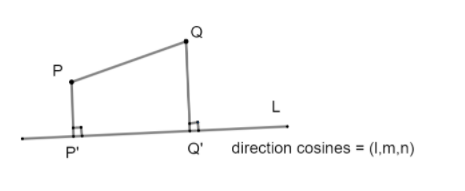
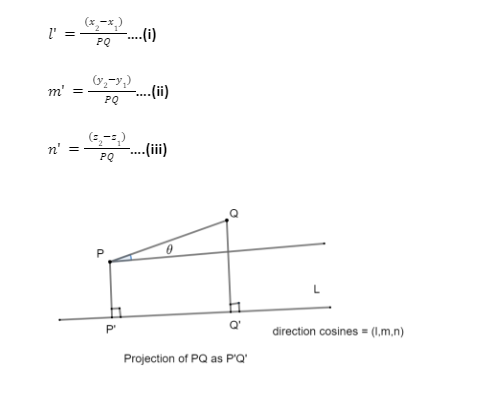
Suppose we have a line segment PQ whose coordinates are x1,y1,z1 and x2,y2,z2, respectively. Let us assume there is another line ‘L’ just below this line PQ whose direction cosines are l,m,n on which we need the projection of line PQ. Projection means, we will be drawing a set of perpendicular lines from both the given point P and Q on the line respectively at P’ and Q’ as shown below:

The next step is to find the length of P’Q’. To do so, let us construct a line parallel to line L and passing through point P. Let us assume this parallel line makes an angle of with PQ. Now, since this line is parallel to L, therefore, its direction cosines will be the same as L, which is l,m,n.
Let us try to calculate this angle .
Now, the direction ratios of the line PQ are x2–x1,y2–y1,z2–z1.
Then, the direction cosines of the line PQ would be l’,m’,n’ defined as below:
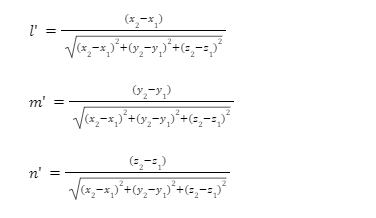
The denominator of l’, m’ and n’ are nothing but the length of line segment PQ, as that is the distance formula to calculate the distance between two points.

Observing the angle in between, we get that P‘Q‘=PQcos , where
cos =ll‘+mm‘+nn‘
P‘Q‘=PQ(ll’+mm’+nn’)
P‘Q‘=l(l’PQ)+m(m’PQ)+n(n’PQ)
Now from equation (i), (ii) and (iii) we have,
P‘Q‘=l(x2–x1)+m(y2–y1)+n(z2–z1)
And this is what we needed to determine.
Therefore, the projection of a line segment PQ whose coordinates are x1,y1,z1 and x2,y2,z2 respectively on the line having the direction cosine as l,m,n is given by
P‘Q‘=l(x2–x1)+m(y2–y1)+n(z2–z1)
Conclusion
In conclusion, the projection of a line segment PQ whose coordinates are x1,y1,z1 and x2,y2,z2 respectively on the line having the direction cosine as l,m,n is given by
P‘Q‘=l(x2–x1)+m(y2–y1)+n(z2–z1)
Here the different possibilities of the coordinates of the line segment and the line can both be taken care of. It is not required for the line segment joining two points to be parallel or perpendicular to the given line. In any case, we can easily calculate the projection.
Although, when the line segment joining two points becomes perpendicular to the line, the projection is nothing but a point on the line.