Trigonometry is one of the subjects that academics from all around the world have been studying for a very long time. The field of astronomy was the impetus behind the development of trigonometry. Since that time, astronomers have made use of it in a variety of ways, such as to determine the distances between the Earth and the planets and stars. In addition to its role in geography and navigation, trigonometry also has other applications.
It is necessary to have knowledge of trigonometry in order to calculate the heights of buildings, create maps, and ascertain the location of an island with respect to the longitudes and latitudes.
What is Height and Distance in Trigonometry?
The height of an object is determined by its position with respect to the vertical plane. A horizontal measurement of an object’s distance from a starting point is what we mean when we talk about distance. The vertical line, the horizontal line, and the imaginary line that is drawn from the observation point to the top border of the object make up the three sides of a triangle that is produced.
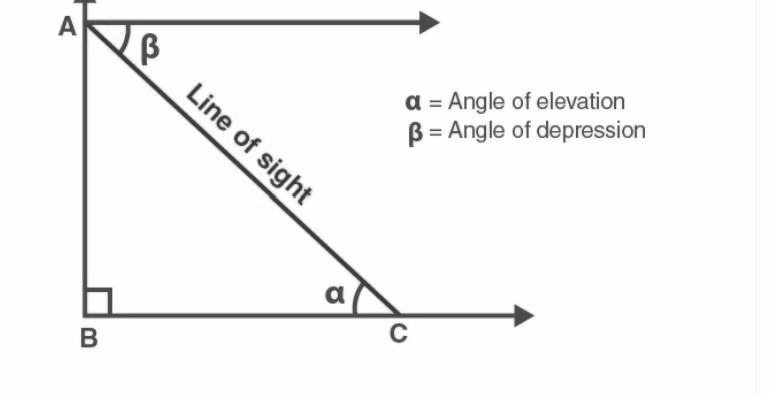
The site of observation is indicated by the letter C in the figure. The value denoted by AB is the height of the object. BC provides information about the distance that exists between an object and an observer. AC will tell you where the line of sight is. The angle of elevation is denoted by the letter alpha, and the angle of depression is denoted by the letter beta. If either of the two quantities (a side or an angle) is known, then the other can be determined by using what is known about the other two quantities. According to the law of alternate angles, the degree to which an angle of elevation is greater than an angle of depression has the same degree of greater magnitude. tan equals height divided by distance.
A method for resolving a height and distance problem
Create a figure that accurately represents the data that was provided, which includes the angles and distances.
If the problem that needs to be solved is a right-angled triangle and one angle and one side of the triangle are known, then trigonometric ratios can be used to identify the other two angles and sides of the triangle.
The equation is known as the sine rule, and it looks like this: a/sin A = b/sin B = c/sin c
Cosine formula i.e., cos A = [b2+ c2 − a2] / 2bc
By equating the two values, you will be able to find the length of the relevant side of either of the two triangles that have a side in common.
Properties of Triangle and Height and Distance
Height and distance are typically used to measure the height of a building from a specific distance when the angle is measured from that point or is measured from the top of the building. This is because the angle is normally measured from the point at which height is measured. We learn about the angle of elevation, the angle of depression, the line of sight, and many other concepts in this article. This idea is mainly applied while determining the following:
a) The amount of space that separates the two banks of the river;
b) The process of determining the distance an aeroplane is from the ground when it is travelling at a steady speed;
c) The distance measured between two different sides of a sea; d) the height measured at the top of a mountain.

The position of the observer is C. The height of the tower may be determined by taking the length of AB, while the length of BC indicates how far away the observer is from the tower. The line of sight is represented here by the letter AC.
Line of Sight is defined as the line that is traced from the eye of the observer to the point that is being seen.
Angle of Elevation: This refers to the angle that is formed by the line of sight when it is horizontal and the viewpoint is elevated above the floor. It is depicted in the figure by the angle denoted by the symbol.
Angle of Depression: This is the angle made when the line of sight from the horizontal point to the horizontal level goes below the horizontal level. It is depicted in the figure by the angle denoted by the symbol.
Therefore, we can write these expressions as follows: sin α = sin ∠BCA = AB/AC and tan α = tan ∠BCA = AB/BC
If we know the value of AB and BC correspondingly, then we can calculate the height of the tower by utilising the tangent angle, provided that we know the value of AB and BC.
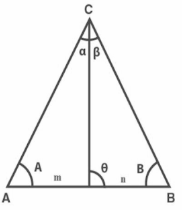
m-n theorem states

(m + n) cot θ = m × cot α – n × cot β
(m + n) cot θ = n × cot A – m × cot B
Trigonometry Applications in Real Life
It is possible that it does not have direct applications in the resolution of actual problems; yet, it is employed in a variety of fields. For instance, trigonometry is utilised in the production of computer music. You probably already know that sound travels in the form of waves, and that the pattern of these waves may be manipulated, through a sine or cosine function, in order to create musical compositions. The following are some examples of situations in which trigonometry and its functions could be useful:
Utilizing Trigonometry to Determine the Height of a Mountain or a Building
When determining the height of a building or a mountain, trigonometry is the method of choice. Using the trigonometric functions, the height of a building may be easily determined by taking into account both the distance from the perspective to the building as well as the elevation angle.
The Use of Trigonometry in Criminal Research
Even the investigation of a crime scene makes use of trigonometry in some capacity. Calculating the path of a projectile using the functions of trigonometry and estimating the factors that led to a collision using trigonometric functions are both useful applications of this branch of mathematics. In addition, it can be used to determine the trajectory of an object’s descent or the angle at which a gun is fired.
The application of trigonometry to marine biology
Marine scientists frequently resort to the use of trigonometry while conducting measurements to determine the intensity of sunlight that has an impact on the process of photosynthesis. Marine biologists are able to make educated guesses about the size of larger species like whales and better comprehend the behaviours of these creatures by employing the trigonometric function and various mathematical models.
The Application of Trigonometry in Navigation
In the process of navigating directions, trigonometry is utilised; it provides estimates regarding where to point the compass in order to obtain a straight direction. It will not be difficult to pinpoint a place with the use of a compass and the trigonometric functions that are used in navigation, and it will also not be difficult to determine distance or to view the horizon.
CONCLUSION
Trigonometry might not have that many applications in everyday life, but learning it might make it easier for you to work with shapes that use triangles. It is a valuable addition to geometry and actual measurements, and as such, it is well worth having a knowledge of the basic concepts, even if you never desire to proceed further in the subject.
Utilizing the tangent function will allow one to arrive at an accurate estimation of the height of the faraway point. We require the horizontal distance from the theodolite to the foot of the distant point, as well as the angle that the foot of the remote point makes with respect to the horizontal, in order to calculate the vertical distance of the remote point using the tangent function.