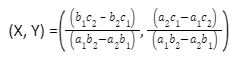
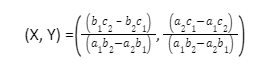
A line is a geometric construct composed of infinite points that extend in both directions indefinitely. It has no depth or width and is completely straight. It is depicted on both sides by little arrows. There are no ends to a line. A line can be formed from any two places that passes through them and extends in both directions.
Intersecting and Non-Intersecting Lines:-
We can divide a pair of line into two parts as follows:
Intersecting Lines
Two or more lines that intersect at the same location are called intersecting lines. On all of these lines, the point of intersection is a common point. It’s worth noting that:
- Regardless of the angle at which the intersecting lines meet, they only meet at one place.
- There can be no more than one point where two straight lines connect.
- Lines that intersect at multiple points are not straight lines.
Non-intersecting Lines
Non-intersecting lines consists of two or more lines that neverintersects. It’s worth noting that:
- Lines that do not intersect cannot meet.
- These types of lines are also termed as parallel lines.
- They always keep the same gap between them and this gap is the distance between the two non-intersecting line.
Point of intersection of two intersectinglines:-
Let the equation of arbitrary two lines be
a1x + b1y + c1= 0
a2x + b2y + c2 = 0
We can also find the location where three or more lines would intersect. But in this case we would discover the solution for the point of intersection of these two lines by solving the two equations.
The formula for finding the point where two lines intersect is:
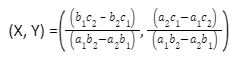
Solved Example
Determine the junction point of the two lines x + 2y + 1 = 0 and 2x + 3y + 5 = 0.
The following are straight line equations:
x + 2y + 1 = 0 and 2x + 3y + 5 = 0
Here, a1 = 1, b1 = 2, c1 = 1
a2 = 2, b2 = 3, c2 = 5
This formula can be used to compute the point of intersection.
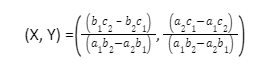
(X, Y)=(-7, 3)
Circle and Line forms in general:-
ax+ by +c=0 can be used to determine the general equation of a line.
Intersection Between Line and Circle:-
As described below, a line can intersect a circle in three different ways:
- If a line intersects or cuts through the circle, we get two points of intersection, as shown in the diagram below. The line intersects the circle at two spots in the diagram above. The secant to the circle is the name given to this line.
- If we draw a tangent line to the circle, as shown in the diagram, we will only have one point of intersection:
- If a line does not touch the circle at all, there will be no point of intersection.
Methods for Calculating the Intersection of a Line and a Circle:-
If we have a line’s linear equation and a circle’s general equation, we can easily determine whether the line crosses the circle. To accomplish this, we must take the following steps:
- Substitute the linear equation for the circular equation. Linear equations are frequently expressed in terms of y. We’ll replace the y-values of the circular equation with the y value of the linear equation.
- To get a quadratic equation, simplify the equation.
- Expand the middle term to factorise the quadratic equation.
- Find the roots, or the x values. To acquire the correct y-values, substitute the values of x in the linear equation.
Conclusion:-
Lines that intersect or cross in a plane are known as intersecting lines. Non-intersecting lines, on the other hand, are two or more lines that do not intersect at any point. Intersecting lines are created when two or more lines meet at a common point. The junction is the point where they cross each other.