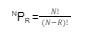
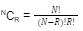
Before we begin to understand permutation and combination in-depth, it is very necessary to understand the meaning of the two words individually. Permutation can be defined as different methods using which the objects can be arranged in a defined order. In other words, when the items that are arranged in an ordered set are rearranged in a linear order, this process is referred to as permutation. People often get confused between permutation and another mathematical term known as combination. However, combination is a technique wherein the order of the selection is not essential in order to determine the collection of item’s possible arrangement. This is also considered as one of the important differences between permutation and combination in mathematics.
What are permutations
Permutation loosely translates to ‘first selection then arrangement’ and combination, on the other hand, means ‘selection’ . Let us illustrate the given definition with a substantial example. Imagine in a class there are seven students; the seven students are being called to the principal’s office. An assistant comes and asks the teacher to send any four of the seven students present in the class to the principal’s office. Imagine on one day the assistant comes and wishes to select four children and ask them to go to the principal’s office and stand in a straight line outside his/her office; this would require selection and then the arrangement of the four students since all four students are unique, there are different ways in which they can be arranged in this straight line outside the principal’s office. This is largely what permutation allows us to do.
Mathematically speaking to illustrate this example of the four students being asked to stand in a straight line outside the principal’s office can be done in 47P Ways. Explaining further, imagine that all four students are to be fit in a box with four compartments – the first slot of the compartment can have seven students choose it, the second slot of the compartment can have six students choose it, the third slot of the compartment can have any five students choose it and likewise the last slot of the compartment is available to 4 students. So the total number of ways in which, out of seven students, we can arrange the four students becomes 7x6x5x4 in other words, is 47P
Permutation Formula
Next, we would look into the permutation formula. Understanding the permutation formula will help us apply permutation in different scenarios and different situations. The basic permutation formula is:
- Wherein R! indicates the number of ways in which a defined number or R number of things can be done.
- NPR Indicates the permutation of ‘R’ things or the number of ways of ‘R’ things out of ‘N’ different things.
Similarly, NCR indicates the different number of ways in which ‘r’ things can be selected out of the available ‘n’ different things. The formula to calculate nCr is given below.
- When it comes to the circular permutation formula, (N-1) helps in calculating the many methods in which the ‘N’ number of things can be put in a circular shape.
- The permutation formula for ‘N’ number of things out of which only ‘R’ things are taken is NR. However, this permutation formula is applicable in cases where repetition is applicable.
Permutation in Circular Arrangements
It will be too naïve of us to only consider permutations that happen in a straight line. In reality, permutations are also circular. Imagine having to arrange ten beads around a garland. How can one do that?
Mathematically, the number of ways in which ‘n’ different things can be arranged in a circle is given by the formula – (N-1)!
The number of arrangements in which ‘N’ things can be arranged on a circular plane (whether clockwise or anticlockwise- as they are considered the same in circular permutations because a circle is a closed loop. So the beginning and the end cannot be correctly demarcated; hence clockwise or anticlockwise arrangements do not entirely matter that much while students are solving questions) and are solved by the formula (N-1)!/2.
Conclusions
A permutation is the mathematical calculation of the number of ways in which a particular set of entities can be arranged but the order of these entities does matter in permutation. Permutations can be both linear and circular in nature. Combinations can be defined as a selection of distinct items from a set, irrespective of the order of these selections.