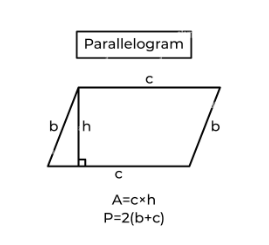
The length of the continuous line formed by the parallelogram’s boundary is the perimeter of the parallelogram. Each of its sides has a unit that is the same as its unit. A quadrilateral is a closed shape made up of four-line segments that are connected together. If the opposite sides of a quadrilateral are parallel and of equal length, the quadrilateral is known as a parallelogram. A parallelogram can be represented by the shapes rhombus, rectangle, and square.
The following are some of the characteristics of a parallelogram:
- In layman’s terms, we can say that the perimeter of a parallelogram is equal to the sum of the four sides of the parallelogram.
- The opposing sides are on an equal footing.
- Angles that are diametrically opposed are equal.
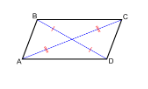
- Diagonals cut each other in half.
- Every pair of adjacent angles is supplementary to the other.
Perimeter of parallelogram formula
In the following situations, the perimeter of a parallelogram can be determined:
- When the positions of two adjacent sides are known.
- Whenever the length of one side and diagonals are known.
- When the base, height, and angle are all known, the problem can be solved.
The following are the perimeter formulas for calculating the perimeter of a parallelogram in each of the following situations:
- When a parallelogram has two adjacent sides, the equation P = 2 (a + b), where a and b are the adjacent sides of the Parallelogram.
- P = 2a + √(2x2 + 2y2 – 4a2), where a is the side of the parallelogram and x and y are the diagonals of the parallelogram, respectively.
- It can be written as P = (2a + 2h)/sinθ, where a denotes a parallelogram’s side and h denotes the height of the parallelogram, and sinθ denotes its angle.

Perimeter of parallelogram formula with sides
The perimeter of a parallelogram is equal to the sum of the lengths of all of its sides combined. In the case of a parallelogram, we already know that the opposite sides are equal. Think of a parallelogram with a pair of adjacent sides that are both the same (then the other pair of adjacent sides will be the same as well, but they will be different from each other).
So the perimeter of the parallelogram is a + b + a + b (or) 2a + 2b (or) 2 (a + b). And is equivalent to The perimeter (P) of a parallelogram with sides a and b is defined as follows:
P is equal to two 2(a + b) units.
Perimeter of parallelogram formula with one side and diagonals
Consider the following parallelogram: a parallelogram with sides a and b and diagonals x and y. Assume that the side ‘a’, the diagonals ‘x’ and ‘y’, and the diagonals ‘x’ and ‘y’ are all known, but the value of the side ‘b’ is unknown, and we are tasked with determining the perimeter of the parallelogram.

In the case of the triangle ABD, the law of cosines is applied.
x2 = a2 + b2 – 2ab cos(angle BAD)
In the case of the triangle ADC, the cosine rule is used.
If y2 equals a2 + b2 – 2ab cos(angle ADC) , then
By combining the two previous equations,
the sum of x2 and y2 is equal to 2a2 + 2b2 – 2ab (cos[angle BAD] + cos[angle ADC])… (1)
We already know that any two adjacent angles of a parallelogram are supplementary (this is a property of parallelograms). So
180° is equal to the sum of angle BAD and angle ADC.
The angle between BAD and ADC is 180°.
Using the cosine formula on both sides,
cos(angle BAD) = cos (180° – angle ADC) = – cos ADC
Using this as a substitute (1),
x2 + y2 = 2a2 + 2b2 – 2ab (- cos[angle ADC] + cos[angle ADC]).
x2 + y2 = 2a2 + 2b2 – 2ab (0)
x2 + y2 = 2a2 + 2b2
We now know what the relationship is between the sides and diagonals of the area of parallelogram is. We will now solve it for ‘b’ because we are not provided with the length of ‘b’.
2b2 = x2 + y2 – 2b2
b2 = (x2 + y2 – 2a2) / 2
b = √[(x2 + y2 – 2a2) / 2]
We now know the lengths of the parallelogram’s sides (‘a’ and ‘b’), and we can use the formula from the previous section to determine the length of its perimeter (P).
P is equal to 2a plus 2b.
P = 2a + 2√[(x2 + y2 – 2a2) / 2]
The equation P = 2a + √[2(x2 + y2 – 2a2)]
P = 2a + √(2x2 + 2y2 – 4a2)
Perimeter of a parallelogram with base, height and angle
Consider a parallelogram in which one of the sides is designated as ‘a,’ the corresponding height is designated as ‘h,’ and one of the vertex angles is designated as ‘a’, as shown in the diagram below. Let us suppose that the unknown side of the parallelogram is represented by the letter ‘b.’ We will begin by determining the value of b, and then we will calculate the perimeter.
When the sin function is applied to the triangle BEC,
sin θ = h/b
b = h /sin θ
As a result, the parallelogram’s perimeter (P) is as follows:
P is equal to 2a plus 2b.
P = 2a + 2h / sin θ
It is not necessary to be a specific angle of the parallelogram in this case. It does not matter what angle the vertex is because any two adjacent angles of a parallelogram are supplementary and sin θ = sin (180° – θ), where θ is an angle.
Conclusion
The perimeter of a circle is equal to the sum of the lengths of all four sides. The total distance outside the geometrical shape of a parallelogram is known as the perimeter of the parallelogram. The length of the continuous line formed by the parallelogram’s boundary is the perimeter of the parallelogram. A quadrilateral is a closed shape made up of four-line segments that are connected together. If the opposite sides of a quadrilateral are parallel and of equal length, the quadrilateral is known as a parallelogram.
The perimeter of the parallelogram is a + b + a + b (or) 2a + 2b (or) 2 (a + b). And is equivalent to The perimeter (P) of a parallelogram with sides a and b is defined as follows:
P is equal to two 2(a + b) units.