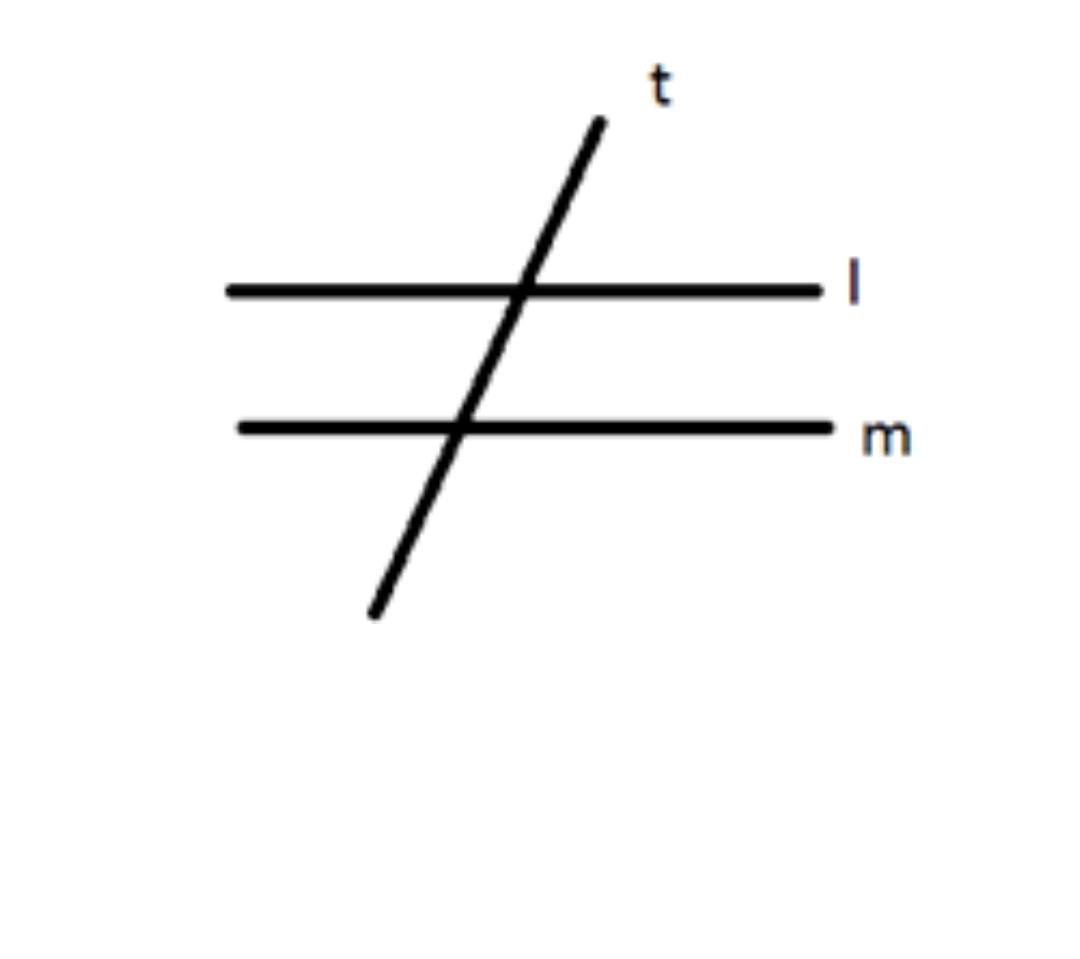
In Geometry, we begin our study of shapes with a focus on lines because they are the most fundamental. When several lines meet in specific places and orientations, nearly all of the shapes that can be made can be described as “formed.” In this chapter, we will study everything there is to know about a pair of lines, including their characteristics and other aspects.
Pair of Lines
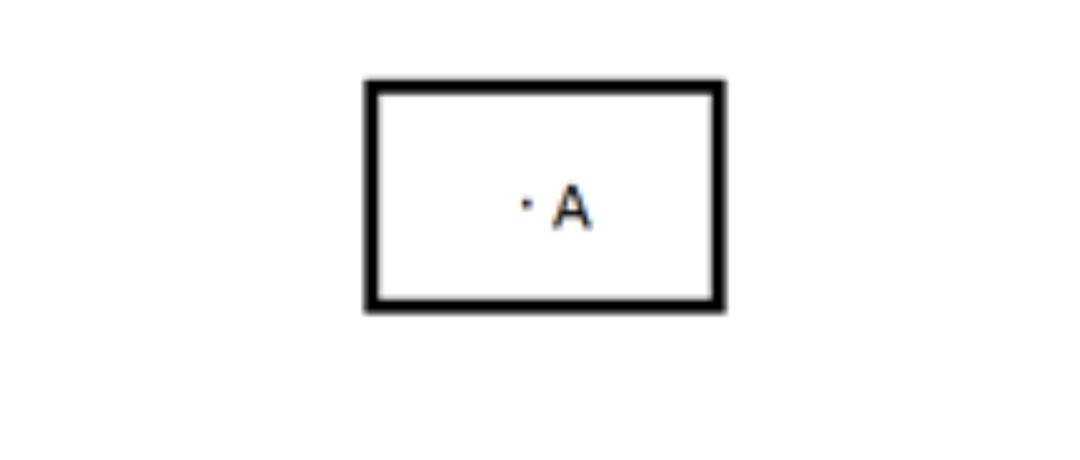
•A point is a precise location, and on a piece of paper, it is denoted by a little dot that is drawn using a pen that has a very fine point. As a result, A is a point, as seen in the image that follows.

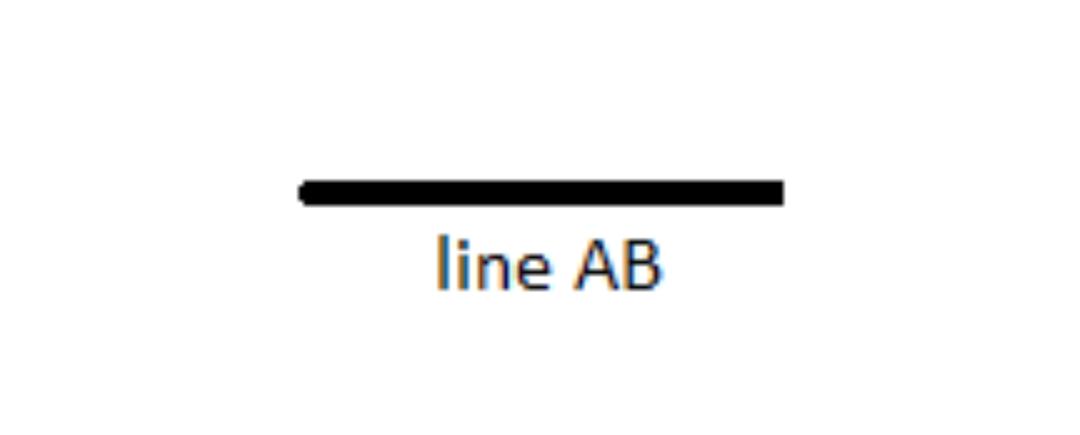
•Line: A line is a collection of points that only has length and not breath or thickness. Lines are drawn using points. A line is a path that is straight and continues on forever in both of its directions. We will refer to it as AB or BA. Take note that a line does not have a terminating point.

Intersecting Lines
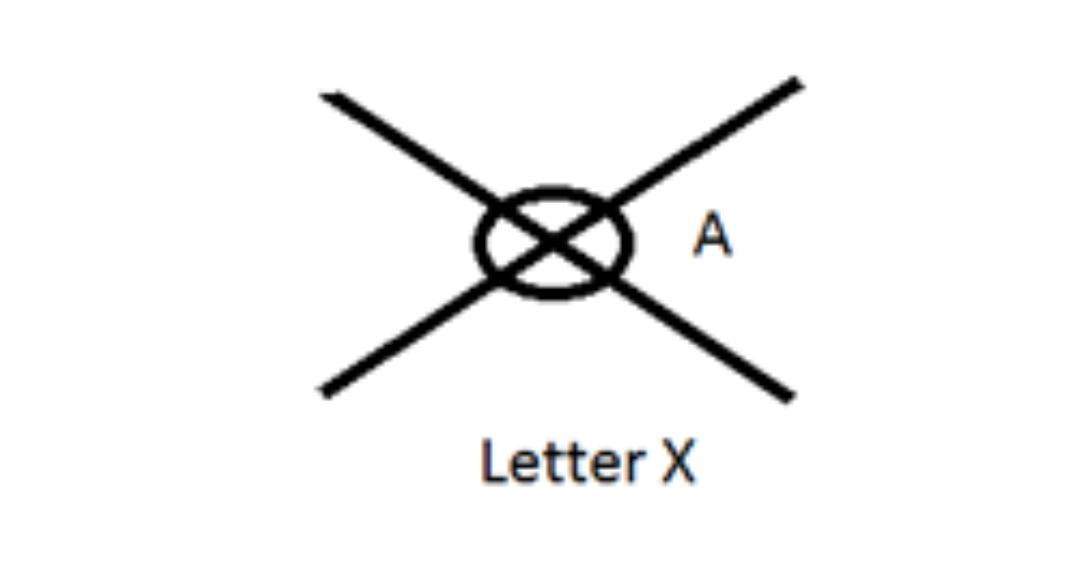
If two lines, line segments, or rays share a point, then the lines, line segments, or rays are said to be intersecting. This point of agreement serves as the intersection of both of their paths. Examples include both sides of a piece of paper that are near to one another, a ruler, a door, a window, and some letters.

Transversal Lines
The term “transversal line” refers to a line that is straight and cuts two or more other straight lines at separate points. Take, for instance, the case of a railway line that intersects with multiple other lines. In the illustration, the line t is a transversal, while the lines l and m are parallel.
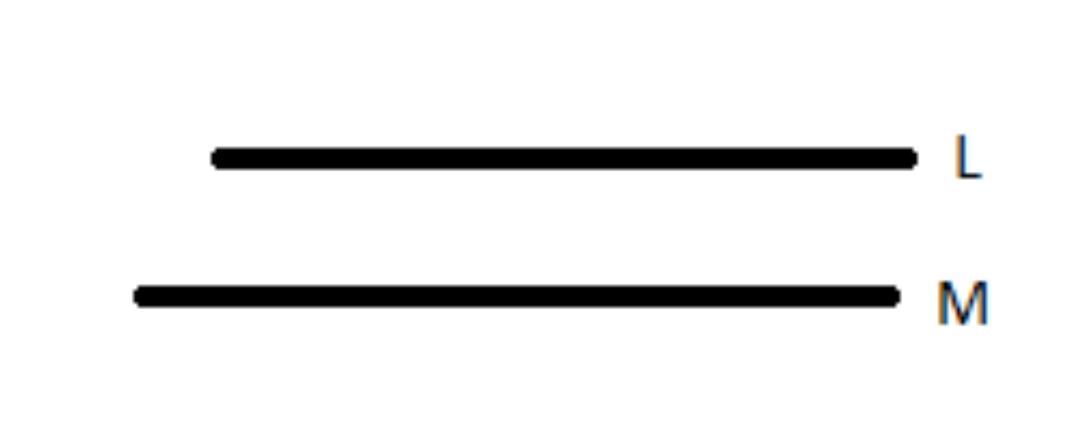
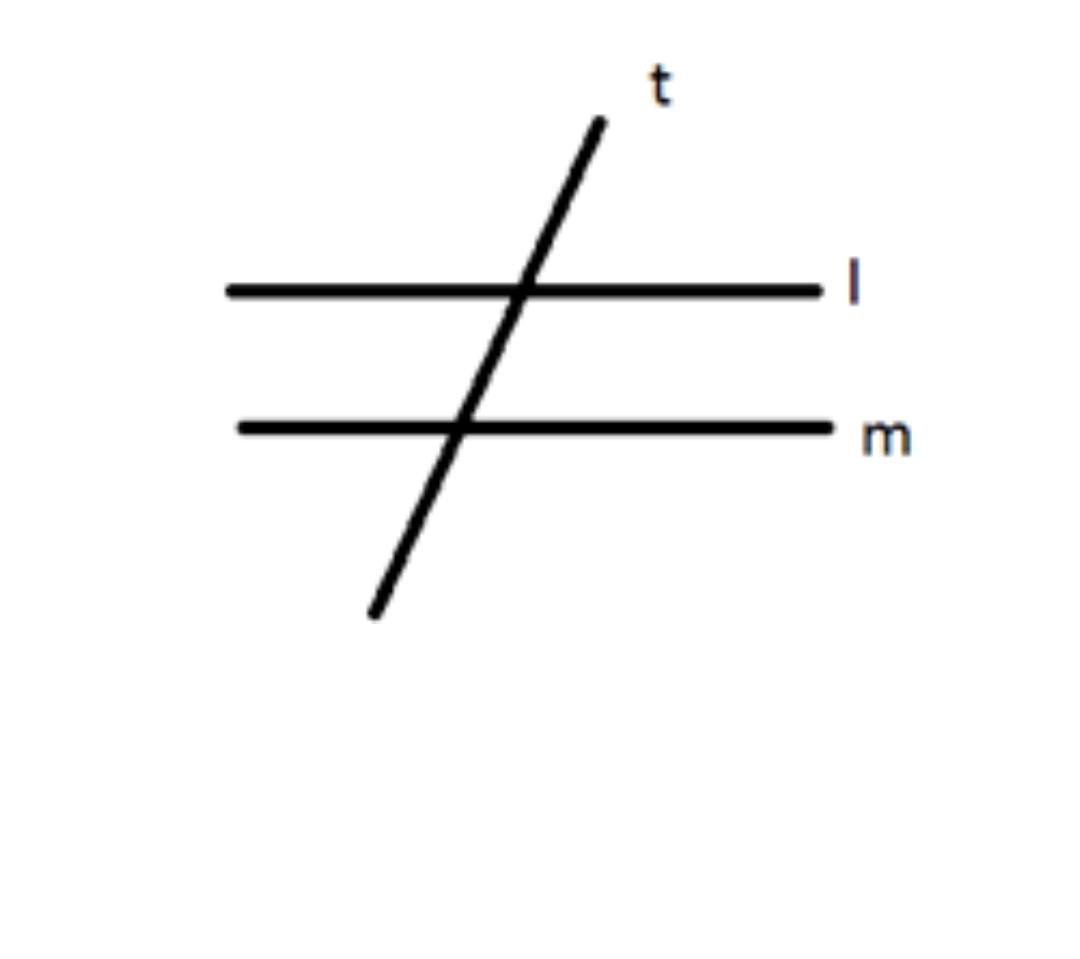 Parallel Lines
Parallel Lines
When two lines lie in the same plane and do not intersect when produced on either side, we say that those lines are parallel to each other. Parallel lines lie in the same plane.

If L and M are two lines that run parallel to one another, then we interpret this as meaning that L runs parallel to M. It is common knowledge that whenever there are two lines in the same plane, those lines will either collide or run parallel to one another. On the other hand, these two lines L and M, which are in the same plane, are considered to be parallel if there is no point at which they intersect, regardless of how far they are extended.
Take note that the distance that separates any two lines that are parallel is always the same. To give only a few examples: a railroad track, the two opposing sides of a chalkboard, the two opposing edges of a door, etc.
Prerequisites for a Pair of Parallel Lines to Exist
When a transversal cuts through two straight lines, the result is a triangle.
if each angle in a pair of adjacent angles is the same, then the two lines drawn straight are parallel to one another.
If the two internal angles are located on the same side of the traversals, which means that they are complementary, then the two straight lines are parallel.
If the two angles that correspond to each other are equal to one another, then the two straight lines will be parallel to one another.
Properties of Parallel lines
•When a transversal line cuts two lines, the lines are said to be parallel if the corresponding angles that are formed are the same for both lines. In most cases, the corresponding angles occupy relative locations within the transversal and are located on the same side of the line.
•Two lines are said to be parallel if the transversal line that cuts them both creates alternate interior angles that are equal to one another. In most cases, the pairs that make up the alternate interior can be found on the inner side of the transversal, although they are located on the sides of the transversal that are opposite one another.
•If the two lines that are cut by a transversal line have equal alternating exterior angles, then the lines are said to be parallel. In most cases, the pairs of alternate external angles can be located on the exterior side of the building, although they face in the opposite direction from one another.
Conclusion
A point is a precise location, and on a piece of paper, it is denoted by a little dot that is drawn using a pen that has a very fine point.A line is a collection of points that only has length and not breath or thickness. Lines are drawn using points.If two lines, line segments, or rays share a point, then the lines, line segments, or rays are said to be intersecting. This point of agreement serves as the intersection of both of their paths.The term “transversal line” refers to a line that is straight and cuts two or more other straight lines at separate points.When two lines lie in the same plane and do not intersect when produced on either side, we say that those lines are parallel to each other. Parallel lines lie in the same plane.