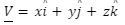
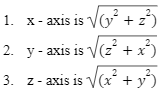
3D geometry is the study of shapes in three-dimensional space using three coordinates: x-coordinate, y-coordinate, and z-coordinate. To discover the exact location of a point in three dimensions, three criteria are necessary. A coordinate system is the technique of determining the position or location of a point on the coordinate plane in three dimensions.
Important Formulae in 3D Geometry
Vector Representation of a Point
A point P (x, y, z) is represented as a vector in 3D space as
![]()
Distance of a point from origin
Using the Pythagorean theorem The distance between P (x,y,z) and the origin O (0,0,0) is
d = √(x2+y2+z2)
Distance of a Point from Coordinate Axes
The distance from the point P (x, y, z) to
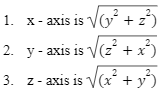
Distance Between 2 Points in Space
Using the Pythagorean theorem The distance between P (x1,y1,z1) and the Q (x2,y2,z2) is
d = √((x2-x1)2+(y2-y1)2+(z2-z1)2)
Point dividing line segment joining two points.
Let R be a point which divides the line segment PQ between two points P (x1,y1,z1) and Q (x2,y2,z2) internally with ratio m:n then the coordinates of R are:
((mx2+nx1)/(m+n), (my2+ny1)/(m+n), (mz2+nz1)/(m+n))
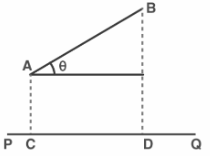
A Line Segment Projected in Three Dimensions
Assume that AB is a line segment. Then its projection on line PQ is ABCosθ

Centroid and Incenter of a Triangle
For a triangle formed with points P (x1,y1,z1), Q (x2,y2,z2) and R (x3,y3,z3), and lengths of sides as a, b and c its centroid is
((x1+y1+z1)/3 , (x2+y2+z2)/3 , (x3+y3+z3)/3)
And its incenter is
((x1+y1+z1)/(a+b+c) , (x2+y2+z2)/(a+b+c) , (x3+y3+z3)/(a+b+c))
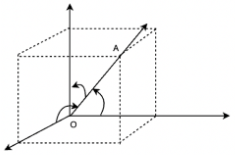
Direction Cosines of a Line
Assume a line OA passes through the origin and forms direction angles α, β, and γ with the x, y, and z-axes, respectively. The directional cosines of the directed line OA are the cosines of these angles cos(α), cos(β), and cos(γ). The line OA traveling through the origin and all of the angles it makes with the coordinate axes are depicted in the diagram below.

Note: The line can extend in both directions, and it can produce two different angles with the coordinate axes. The line makes α, β, and γ and their supplements π-α, π-β, and π-γ with the coordinate axes. The directional cosines’ indications will now be flipped. We chose to make it a directed line in order to have unique directional cosines.
Let’s say the lines’ directional cosines are l, m, and n.
Ratios of Direction
Direction ratios of the line are numbers that are proportional to the line’s direction cosines. The directional cosines of the lines are assumed to be l, m, and n. Let’s say the line’s directional ratios are a, b, and c. Then,
l = k × a, m = k × b and n = k × c
Where k is any constant.
Conclusion
Three-dimensional space is a geometric setting in which the position of an element is determined by three values. This is how the term dimension is commonly used. A tuple of n numbers can be thought of as the Cartesian coordinates of a point in n-dimensional Euclidean space in mathematics.