
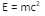
Through precise measurement, it has been found that the mass of a particular atom is always a little less than the sum of the masses of the individual neutrons, protons, and electrons of which the atom consists. Subtracting the sum of the mass atom’s constituents from its mass, we get a mass defect ( ∆ m). We will learn about the topic with this study material notes on mass defects.
Mass-Energy Relation
Albert Einstein firstly proved the mass-energy relation. He put forward the equation
E = mc2. This equation provides the relationship between the mass and the system’s energy.
This relation also depicts that the object at a stationary state has energy. The energy is in the form of potential energy and, in some cases, chemical and thermal energy.
There is the various significance of mass-energy relations. The most important ones are in the field of nuclear fission and fusion. The mass-energy relation can be used to find the nuclear binding energy.
Binding Energy
Binding energy is the energy required to divide the nucleus of the atoms into its parts. This energy is equal to the energy holding the particles together.
From the binding energy, it is found that there is a significant difference between actual mass and expected mass. It is because the mass of the nucleus is always less than the separate masses of protons and neutrons. It happens as energy is always lost during the formation of the nucleus.
Mass Defect
When the nucleus is formed, some energy is lost, which has mass. This mass is known as a mass defect. The mass defect means that the actual mass of the nucleus is not equal to the mass of protons and neutrons. The mass defect can be calculated using an equation.
While calculating the mass defect, it becomes vital to use precise mass measurements. There is only a slight difference between the atom’s mass and its parts. Rounding off the masses of atoms and particles to three or four significant digits before the calculation will result in a calculated mass defect of zero.

Nuclear Binding Energy
The mass defect can calculate the nuclear binding energy. The mass is converted into energy using the formula:
![]()
Nuclear binding energy is used to determine whether fission or fusion of the nucleus will take place. For stable nuclei, the binding energy’s value is positive. When the nucleus is composed of more than one nucleon, its energy composition is also termed nuclear binding energy.
The nuclear binding energy is liberated at the time of three exothermic processes such as:
- Radioactive decay is when neutrons or protons decay by emitting electromagnetic radiation or gamma rays.
- Fusion is the process of fusing two atomic nuclei to generate heavier nuclei.
- Fission is the process of splitting up a nucleus into two lighter nuclei.
Conclusion
The binding energy is required to split the nucleus into its particles, such as neutrons and protons. However, it has been found that the mass of the nucleus is never equal to the sum of the masses of neutrons and protons. It is so because the energy is always lost during the formation of the nucleus, and it has mass.
Thus, the mass lost during the reaction is known as a mass defect. This mass is then converted into energy using mass-energy relation. We can calculate the mass defect using the formula provided in this study material notes on the mass defect.