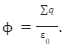


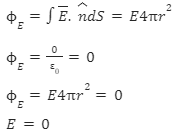
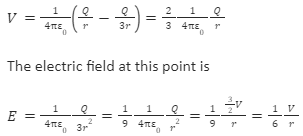
One of the most significant fields of physics is electrostatics, which deals with a charged particle in rest mode (i.e., in a static position). In 1976, Dutch physicist Pieter van Musschenbroek of the University of Leiden made an unintentional discovery and explored the influence of electrostatics. Static electricity (also known as electrostatic electricity) is a natural phenomenon that dates back to prehistoric times. It was later discovered by the French physicist Charles Augustin de Coulomb, well-known for theorising Coulomb’s law.
A charged hollow sphere is a metallic sphere with a static charge on its surface and does not conduct current.
A Spherical Shell of Charge
Note that a uniformly charged spherical shell interacts with external fields in a similar manner to a point charge (as long as it stays uniformly charged).
- The shell must be spherically symmetric and thin enough to ignore any thickness-related effects.
- It makes no difference what material the spherical shell is composed of as long as the charge is spread in a thin, spherically symmetric shell.
- The electric field of distributed charges as produced by a uniformly charged spherical shell, cylinder, or plate can be measured using Gauss’s law. We will use Gauss’s law to calculate the electric field of an evenly charged spherical shell.
According to Gauss’s law,
Any hypothetical closed surface’s net electric flux is equal to 1 times the closed surface’s net electric charge.
“Gaussian Surface” is the name given to the hypothetical closed surface.
If the net charge inside a Gaussian surface is q, the net electric flow across the surface is =
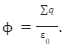
Electric Field Of Charged Hollow Sphere
- Assume a conductor is used to create a hollow sphere with a radius r.
- The conducting hollow sphere is positively charged due to the +q coulomb charges.
- If the sphere has the same density all around its surface, the +q charge will be evenly distributed.
- As a result, the entire system is symmetric. The direction of the electric field will be radially outwards or inwards, based on this symmetry.
- The symmetry will be lost otherwise. As the charges are positive, any positive point charge that comes close to the sphere will repel it.
- As a result, the movement will be radially outwards. Due to the symmetry, we can also deduce that the magnitude of the electric field will be equal to the equidistant distances from the centre.
Let us now consider a hypothetical sphere with the same radius as the charged sphere and the same centre.
Our Gaussian Surface is the outer spherical surface, and q=+q is the net charge inside the Gaussian surface. The total electric flux via the Gaussian surface, according to Gauss’s

Through the surface, E remains constant. Because the distance between all places on the surface and the centre is the same. We previously stated that, due to symmetry, E will remain constant in all equidistant locations from the centre. As a result, E can be extracted from the integration sign.

Consider a hollow sphere with a radius of R and a charge of Q. Consider a sphere with a point P inside it and a centre O that is r=OP (where r < R) as the Gaussian surface to find the electric field inside the sphere.
The electric flux through the Gaussian surface:
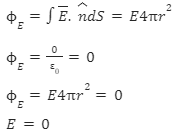
Examples: If r is the radius of a hollow charged metal sphere, what will be the electric field intensity at a distance of 3r from the centre if the potential difference between its surface and a point at a distance of 3r from the centre is V?
Ans: The charge Q on a hollow metal sphere is evenly distributed on its surface, indicating that the potential and electric field outside the sphere are the same as for a point charge Q placed in the centre of the sphere.
Thus, the potential difference between the surface and the point at a distance of 3r is
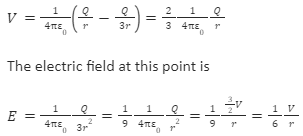
Electrostatics
Electrostatics is defined as the study of electromagnetic phenomena that only occur when no moving charges are present. This phenomenon will only become apparent once the system has reached a stable equilibrium condition.
Conclusion
A charged hollow sphere contains a static charge on the surface of the sphere, i.e., it is not conducting current. The term “electrostatic” comes from the fact that charged particles are constantly in a fixed or resting state. Electrostatics refers to the current that carries charged particles in a static model. In electrostatics, there are three fundamental laws. Similar charges repel each other, dissimilar charges attract each other, and charged items are drawn to neutral objects.