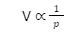
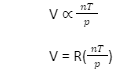

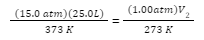
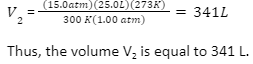
Gases are one of the fundamental states of substances. Gas is a collection of molecules that are separated by a significant distance. The ideal gases are those in which the molecules collide in elastic ways. In these perfect gases, there are no intermolecular attraction forces. However, there are no such things as perfect gases in reality.
Meaning of Ideal Gas
The particles in an ideal gas do not attract or repel one another, nor do they take up any space (the particles do not have volume). The macroscopic properties of ideal gases are related to the ideal gas law (PV = nRT). Although no gas is completely perfect, the ideal gas law provides a decent approximation of real gas behaviour in many situations. Under specific pressure and temperature conditions, gases perform ideally. Thus, at room temperature, an ideal gas would not form a liquid due to all of these assumptions.
Properties of an Ideal Gas
An ideal gas has a number of properties, and real gases often behave extremely similar to ideal gases. The following are some of the properties of an ideal gas:
- A high number of similar molecules make up an ideal gas.
- Compared to the volume occupied by the gas, the volume occupied by the molecules is insignificant.
- The molecules move in a random pattern, obeying Newton’s Laws of Motion.
- The molecules are only subjected to forces when they collide; any collisions are fully elastic and take only a fraction of a second.
- The average kinetic energy of all gases at a given temperature is the same.
- Gas molecules that are lighter travel quicker than heavier molecules.
- The mass of an ideal gas can be ignored in the equation because it has none; this is because an ideal gas is referred to as a particle, which has no mass.
Characteristics of Ideal Gas
The critical characteristics of an ideal gas are as follows:
- They are made up of molecules and atoms, which are tiny particles.
- Although the particles individually have no volume, the gas as a whole does. It signifies that the particles present in the gas have a very small volume. As a result, all the particles now have some volume. However, because of how small it might be, this condition does not apply to all gases.
- The forces of attraction between the gas particles are thought to be insignificant. The forces of attraction are weak, but they exist. As a result, this requirement does not apply to all gases.
- Individual gas molecule collisions are described as fully elastic collisions. We also know that no collision is perfectly inelastic or elastic at the same time. As a result, this requirement does not apply to all gases.
- The gas particles will always move in a random pattern. This is because when gas particles move, they expand. This is true for all gases.
The Ideal Gas Law
There are three laws that have been propounded according to which ideal gases behave. These are as follows:
- Charles’s Law: When the pressure is held constant, Charles’s Law describes the precisely proportionate relationship between the volume and temperature (in Kelvin) of a certain amount of gas. Thus, the derivative of Charles’s Law can be represented as follows:
V∝ T
- Boyle’s Law: According to Boyle’s Law, the volume of a gas is inversely proportional to its pressure at any constant temperature and number of moles. The derivative can be expressed in the following way:
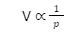
- Avogadro’s Law: At constant pressure and temperature, the volume of a gas is directly proportional to the number of its moles, according to Avogadro’s Law. The derivative can be expressed in the following way:
V∝ n
Thus, we can derive the Ideal Gas Law based on the different laws of ideal gases mentioned above. It can be iterated as follows:
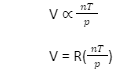
Here, R refers to the proportionality constant.
Thus, we derive the following answer by rearranging the previous equations:
pV = nRT
Thus, R is the universal gas constant, which is the same for all gases. The ideal gas equation is the solution to the above equation. As a result, n moles of any gas will have the same volume at constant pressure and temperature.
Solved Example
A chemist has gas at 15.0 atm pressure, at a volume of 25.0 L, and a temperature of 300 K. Find out the volume of the gas at standard temperature and pressure.
Note that the Standard pressure is 1.00 atm, and the standard temperature is 0 oC (or 273 K).
Solution:
We have been given the following values:

Thus, we will substitute these variables into the ideal gas law equation, as follows:
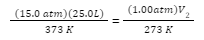
We will now find the volume, V2, by multiplying both sides by the standard temperature, 273 K and dividing both sides by the standard pressure 1.00 atm:
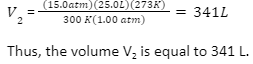
Conclusion
An ideal gas has a number of properties, and real gases often have a behaviour extremely similar to that of ideal gases. There are three laws that have been propounded according to which ideal gases behave – Charles’s Law, Boyle’s Law, and Avogadro’s Law.