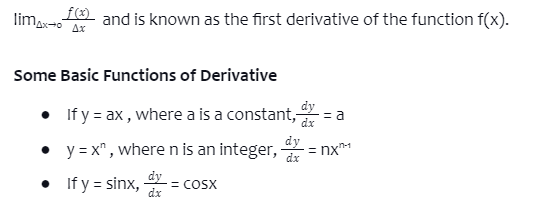







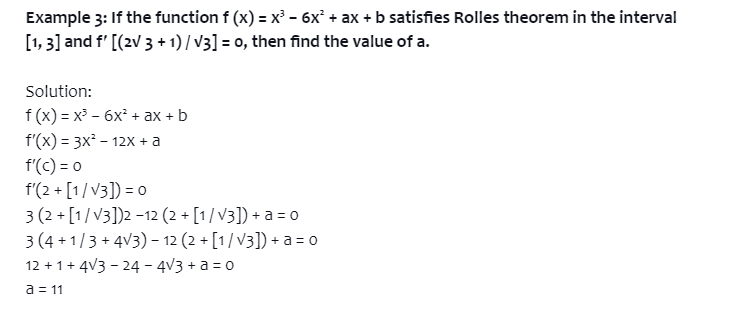
Differentiation is much needed to find the rate of change. It all starts with the differentiation of a single variable into a higher order of variables. The slope of a tangent line indicates a graph of the function at any point. Differentiation applies to several different variables. Differentiation can be done for implicit functions by taking the one in two variables as variables and the other as a function.
For example, the derivative of a function z = f(y), which means the rate at which the value of y changes concerning the value of z.
The general representation of a derivative is d/dx
For example , d/dy(1) = 0
This means differentiating 1 with respect to y gives 0 as a result.
Differentiate a Function
Consider the function f(x) as a function of the independent variable x. The independent variable x is caused by a tiny change in the independent variable Δx. The function f(x) undergoes a similar modification Δf(x). The ratio is:
Δf(x)Δx
is a measure of f(x) of change in relation to x.
As Δx approaches zero, the ratio’s limit value is
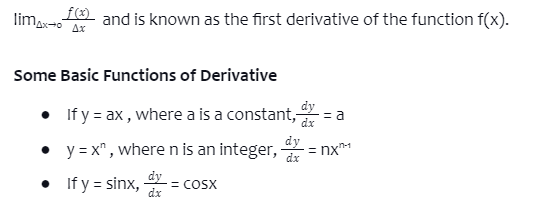

Some Standard Substitution
The following are some of the most useful substitutes for simplifying the provided mathematical expressions and making the differentiation and integration process easier.


Rules of Derivatives
The rules of the derivation include:
- Sum rule
- Difference rule
- Product rule
- Quotient rule
Consider, f(x) and g(x) are two functions whose derivatives are defined in a common domain. Now, we can define the following rules of differentiation for the functions f and g.

Differentiation of Trigonometric Functions
The differentiation of trigonometric functions refers to the process of determining the derivatives of trigonometric functions. A trigonometric function can be differentiated by calculating its rate of change with respect to a variable. Differentiation formulas for the six trigonometric functions can be employed in a variety of applications of the derivative.
Cosine (cos x), tangent (tan x), cotangent (cot x), secant, and cosecant are the six basic trigonometric functions formulas. The derivatives and proofs of trigonometric functions can be found in this article. There are numerous uses for the differentiation of trigonometric functions in various domains, including electronics and computer programming.
Defining the rate of change of trigonometric functions with respect to a variable angle is a mathematical technique known as differentiation in trigonometry. Quotient rule can be applied to the differentiation of trigonometric functions to obtain the derivatives of sin x and cos x. Here is the list of trigonometric functions formulas:



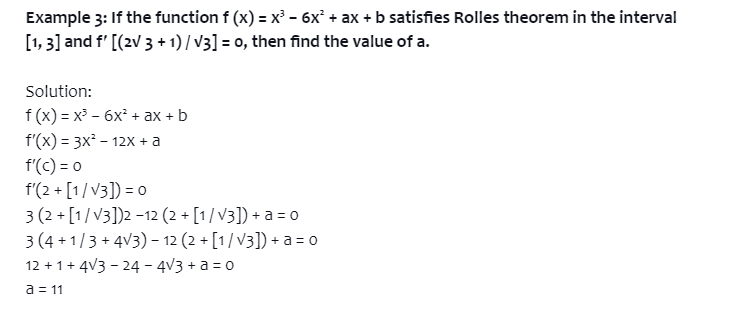
Conclusion
Differentiations are the first step to Calculus. Before learning differentiation and integration, fundamental concepts like derivatives and limits must be understood. The role of derivatives in mathematics will help you understand their importance in fields like engineering. Even in other new-age fields, differentiation has become indispensable. Basic knowledge of derivatives will make you comfortable with more complex concepts of differential calculus and later integration.