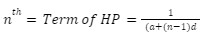
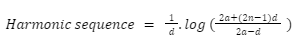
A harmonic progression is a mathematical progression that is created by multiplying an arithmetic progression by its reciprocals. A sequence is equivalent to a harmonic progression when each term is the harmonic mean of the neighbouring terms.
The reciprocal of the terms of an arithmetic progression yields a harmonic progression. 1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), 1/(a + 4d),…1/(a + (n – 1)d are the terms of a harmonic progression. We can compute the nth term, the sum of n terms of the harmonic progression, similarly to the arithmetic progression.
Definition of Harmonic Progression
“A harmonic progression (H.P.) is a set of real numbers that do not contain 0 and are derived from the reciprocals of an arithmetic progression.” “In harmonic progression, any term in a series is considered the harmonic mean of its two neighbours.”
“A series of terms is called a Harmonic progression series when the reciprocals of elements are in arithmetic progression.”
If p, q, r, and s are in arithmetic progression, then 1/p, 1/q, 1/r, and 1/s are all in harmonic progression.
For example:
1/10, 1/12, 1/14, and 1/16 are the first four numbers in the series. . . . . . . . 10, 12, 14, 16, are the reciprocals of the given series. . . . . . . The first term is ’10,’ and the common difference is ‘2.’ The series is clearly in Arithmetic progression.
As a result, the series is moving in a Harmonic manner.
Harmonic Progression Formulas
The formulas below can be used to calculate various harmonic progressions.
Harmonic Progression nth term
It’s the reciprocal of the nth term of the arithmetic progression. The nth term of the harmonic progression is the reciprocal of the sum of the first term and the (n – 1) times of the common difference. Any of the harmonic sequence’s terms can be found using the nth term.
![]()
Harmonic mean
The harmonic progression is multiplied by its reciprocal to create the arithmetic progression. We must first find the first term and the common difference in order to solve the remaining problems. The nth term or the sum of n terms can be found by solving the harmonic progression.
The harmonic progression is made by taking the reciprocal of the terms in the arithmetic progression. If the given terms in the arithmetic progression are a, a + d, a + 2d, a + 3d,…,
then the harmonic progressions (or harmonic sequence) terms are:
1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), 1/(a + 4d),…… The first term is a, and the common difference is d. The values of a and d are both non-zero.
There are an infinite number of harmonic progressions.
In a harmonic progression, any series term is the harmonic mean of its neighbouring terms.
Harmonic Mean = n /[1/a + 1/(a + d)+ 1/(a + 2d) +1/(a + 3d) +…]
Two terms a and b have a harmonic mean =2ab/(a+b)
nth-term harmonic sequence sum
![]()
Conclusion
“The reciprocals of an arithmetic progression form a harmonic progression, which is a sequence of real numbers,” we conclude in this article. Each term is the harmonic mean of its two neighbours.” There are an infinite number of harmonic progressions. When the number of raindrops is calculated using harmonic progression, the illusion is created that the number of raindrops can be estimated when the series is infinite. In mathematics, physics, business, and other fields, harmonic progression and the harmonic mean have numerous applications.