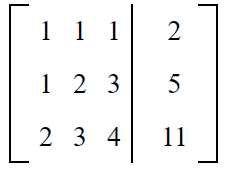
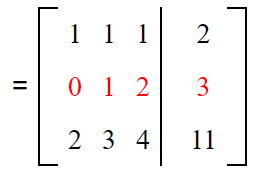
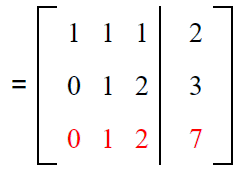


The Gauss elimination in linear and multilinear algebra is a process for finding the solutions to a system of simultaneous linear equations by first solving one of the equations for one variable and then substituting the expression into the remaining equations. The result is a new system in which the number of equations and variables is one less than the original system. The same procedure is applied to another variable and the process of reduction continued until there remains only one equation, in which the only unknown quantity is the last variable. Solving the equation makes it possible to “back substitute” the value in an earlier equation that contains this variable and one other unknown in order to solve for the other variable. This process is continued until all the original variables are evaluated. The whole process is greatly simplified using matrix operations, which can be performed using computers.
Gauss Elimination Method-
The Gaussian elimination method also called the row reduction algorithm for solving the linear equations systems. It consists of a sequence of operations performed on a corresponding matrix of coefficients. We can also use this method to estimate either of the following given below:
The rank of the matrix
The determinant of the given square matrix
The inverse of any invertible matrix
To perform row reduction on a matrix, we have to complete a sequence of elementary row operations to transform any matrix till we get 0s (i.e., zeros) on the lower left-hand corner of that matrix as much as possible. That means the obtained matrix will be an upper triangular matrix. There are three types of elementary row operations; they are as follows:
Swapping two rows and it can be expressed using the notation ↔, for example- R2 ↔ R3
Multiplying the row by a nonzero number, for example, R1 → kR2 where k is a nonzero number
Adding a multiple of one row to the other row, for example, R2 → R2 + 3R1
The obtained matrix will be in the row echelon form. The matrix is said to be in reduced row-echelon form when all of the leading coefficients are equal to 1, and every column containing a leading coefficient has zeros somewhere else. This final form will be unique; in other words, it is independent of the sequence of row operations. We can understand this in a better way with the help of the examples given below.
Gauss Elimination Method With Example-
Let’s have a look at a gauss elimination method example with the solution.
Question: Solve the following system of equations:
x + y + z = 2
x + 2y + 3z = 5
2x + 3y + 4z = 11
Solution:
The Given system of equations are:
x + y + z = 2
x + 2y + 3z = 5
2x + 3y + 4z = 11
Now Let us write these equations in matrix form.
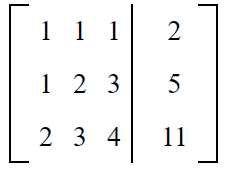
Subtracting R1 from R2 to get the new element of R2, i.e. R2 → R2 – R1.
From this we get,
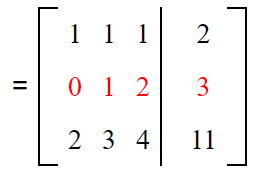
Now let us make another operation as R3 → R3 – 2R1
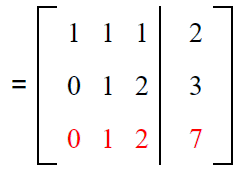
Now subtract R2 from R1 to get the new elements of R1, i.e. R1 → R1 – R2.

Subtract R2 from R3 to get the new elements of R3, i.e. R3 → R3 – R2.

Here,
x – z = -1
y + 2z = 3
0 = 4
Hence, there is 0 solution for the given system of equations.
Solving the System of Equations-
Solving a system consists of finding the value for any unknown value that verifies all equations that make up a system-
There is a single solution, then it is said that the system is a Consistent Independent System (CIS).
There are many solutions, then it is said that the system is Consistent Dependent System (CDS)
If there are no solutions, then in that case it is called Inconsistent System (IS).
Thus, solving the system of equations by the Gaussian elimination method consists of elemental operations in rows and columns of the augmented matrix to get its echelon form.
Conclusion:
The Gauss elimination in linear and multilinear algebra is a process for finding the solutions to a system of simultaneous linear equations by first solving one of the equations for one variable and then substituting the expression into the remaining equations. The result is a new system in which the number of equations and variables is one less than the original system. The same procedure is applied to another variable and the process of reduction continued until there remains only one equation, in which the only unknown quantity is the last variable. Solving the equation makes it possible to “back substitute” the value in an earlier equation that contains this variable and one other unknown in order to solve for the other variable. This process is continued until all the original variables are evaluated. The whole process is greatly simplified using matrix operations, which can be performed using computers.