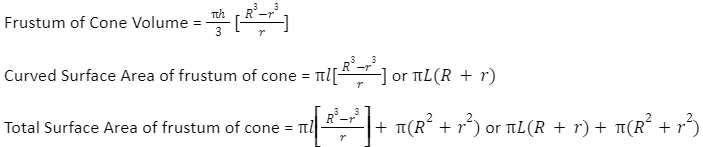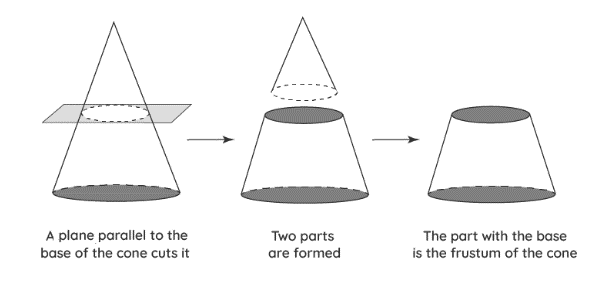
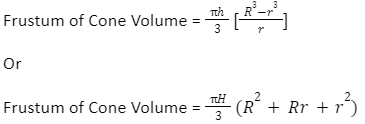


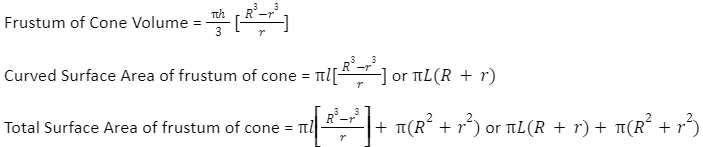
When a cone is divided by a plane which is parallel to its base, the portion of the cone that still has its base is known as the frustum. Cones and pyramids are examples of frustums, which are also referred to as truncated shapes.
Frusta is the plural form of frustum. The portion of a cone that results from splitting a cone in half with a plane is known as the frustum of a cone. The lower portion of the cone forms a frustum while the upper portion of the cone maintains its shape. The cone must be split horizontally, parallel to the base, to obtain this portion of the correct circular cone. These two artworks are clearly different in terms of their area and volume. A glass tumbler looks like a cone without the pointed end. A tumbler is comparable to the frustum of a cone, it can be argued.
Cone
A cone is a common example of a three-dimensional geometric shape, featuring a flat surface and a curved surface that is oriented upward. The flat portion of the cone is referred to as the base, while the pointy end is termed as the vertex.
Frustum of Cone
When a cone is split in 2 parts by a plane which is parallel to the base of cone, then the portion of the cone without a vertex is known as the frustum. Truncated cone is another term used for the frustum of a cone. The cone’s frustum has volume and surface area just like any other 3D form.

Frustum of Cone Properties
The method by which a frustum of a cone is produced determines its qualities. These are a cone’s frustum’s characteristics.
The base of a cone, rather than the equivalent cone’s vertex, is contained in the frustum of the cone
A cone’s height and two radii determine its frustum (corresponding to 2 bases)
The perpendicular or normal distance between the centres of the 2 frustum bases determines the height of frustum of the cone
The frustums that are generated from a right-circular cone would also be right-circular
Frustum of Cone Volume
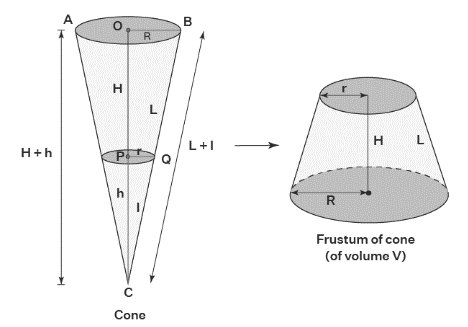
The quantity of space inside a cone’s frustum is known as its volume. The volume of the frustum of a cone is measured in cubic units like m3, cm3, in3, etc., much like the volume of any other form. Think of a cone with a base radius of R and a height of H + h. Assume that the cone breaks down into a frustum with a large base radius (R) and a tiny base radius (r). Suppose L and L +l represent the cone’s and frustum’s respective slant heights. The volume of the cone’s frustum can then be calculated using one of the following formulas.
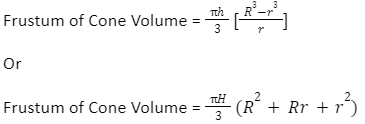

Surface Area of Frustum of Cone
By summing the areas of all of its faces, the surface area of the cone’s frustum is determined. It is measured in square units like m2, cm2, etc. because it is an area. There are two categories of areas in the cone’s frustum.
The area of the frustum’s curved surface is known as the curved surface area (CSA) (or Lateral Surface Area, or LSA).
Total Surface Area or TSA: In other words, CSA plus the sum of the areas of the circular bases, equals the total area of all its faces.
Think of a cone with base radius R, height H + h, and slant height L + l. Assume that the cone is transformed into a frustum with height H, tiny base radius r, large base radius R, and slant height L. Here are the calculations for a cone’s frustum’s total surface area (TSA) and curved surface area (CSA).
![]()
Or
Curved Surface Area of frustum of cone = πL(R+r)
Using the area of circle formula, the base areas of frustum of cone are determined to be R2 and r2. Thus, the total base area is equal to (R2 + r2). Therefore, the cone’s frustum’s total surface area (TSA) is given as;

Or
Total Surface Area of frustum of cone = πL(R + r) + π(R2+r2)
Conclusion
The definition of a cone was provided in the article above. Additionally, we have analysed the cone’s frustum and its shape. We acquired formulas for calculating the surface area and volume of a cone’s frustum.
The area between cutting plane & the cone base when a right circular cone is severed by a plane which is parallel to its base is referred to as the frustum of the cone.