
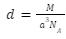
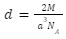
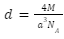
Solids have a structure that may be compared to that of a three-dimensional piece of wallpaper. A regular repeating design runs from one edge to the other on wallpaper. The repeating pattern in crystals is similar, but it stretches in three dimensions from one edge of the solid to the other. Solids have a structure that may be compared to that of a three-dimensional piece of wallpaper. A regular repeating design runs from one edge to the other on wallpaper. The repeating pattern in crystals is similar, but it stretches in three dimensions from one edge of the material to the other.
Simple Cubic Unit cell
In a simple cubic structure, the simplest repeating unit is the simple cubic unit cell. A lattice point defines each corner of the unit cell, where an atom, ion, or molecule can be located in the crystal. The edge of a unit cell, by convention, always links comparable locations. As a result, each of the unit cell’s eight corners must contain an identical particle. Other particles may be present on the unit cell’s edges or faces, as well as within the unit cell’s body. However, the unit cell must have at least eight equivalent particles on each of its eight corners to be categorised as simple cubic.
Body Centred Unit Cell
In a body-centred cubic structure, the body-centred cubic unit cell is the basic repeating unit. On the eight corners of the unit cell, there are eight identical particles once again. In the heart of the unit cell’s body, however, there is a ninth identical particle.
Face Centred Unit Cell
The face-centred cubic unit cell begins with identical particles in each of the cube’s eight corners. However, the same particles are found at the centres of the six sides of the unit cell, totalling 14 similar lattice points.
Density of Different Unit Cells
Density is a basic aspect that has a direct relationship with an object’s mass.
The term “density” refers to a measurement of comparative compactness that can be demonstrated as a substance’s mass per unit volume. Various materials or substances have different densities. The Greek letter rho () denotes the density. Density is calculated using the following formula:
ρ=m/V
The mass of the unit cell can be calculated by multiplying the total number of atoms present in the unit cell and the mass of each atom.
So, the mass of the unit cell can be written as: Mass=z×m
Here, z is the atomic number and m is the mass of the atoms.
The mass of the atoms present in the unit cell will be calculated as:

Density of Primitive Unit Cells
The number of atoms in a primitive unit cell, z, is equal to one. As a result, density is expressed as:
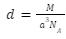
Density of Body Centred Cells
The number of atoms in a body centred cell z, is equal to two. As a result, density is expressed as:
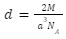
Density of Face Centred Cell
The number of atoms in a face centred cell z, is equal to four. As a result, density is expressed as:
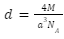
Conclusion
Crystal structure is a depiction of the orderly organisation of atoms, ions, or molecules in a crystalline substance used in crystallography. The symmetry patterns that recur in the major directions of three-dimensional space in matter are caused by the inherent nature of the component particles, resulting in ordered structures.
The smallest collection of particles in the material that makes up this repeating pattern is the structure’s unit cell. The unit cell reflects the complete crystal’s symmetry and structure, which is built up via repeated translation of the unit cell along its fundamental axes.