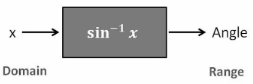

If the lengths of two of the sides of a right triangle are known, then the inverse trigonometric functions sin-1(x), cos-1(x) , and tan-1(x) can be used to determine the unknown measure of one of the triangle’s angles.
The values that can be used in a function are referred to as the function’s domain. The domain of a function is the set of values that can be used. The x values of a function such as f are contained in this collection (x).
The set of possible values that are assumed by a function is referred to as the range of the function. Following the input of a z value, the function generates the values that are contained within this set. They are referred to as the y values.
Domain of a Function
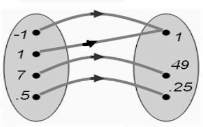
The range of possible values for the variable x that is used to define a function is referred to as its domain. In the image that follows, the domain may be seen in the oval on the left. The function returns a value denoted by f(x) for each individual that is a part of the domain. The collection of values that are returned by the function is referred to as the range of the function, and an illustration of those values can be found in the oval on the right-hand side of the following picture. A relation is said to be a function if it accepts the values from the domain as its inputs and returns those values as its outputs. The rule that governs a function is that there must be exactly one output for every single input.
Because each input is mapped to exactly one output, we can also identify that it is a function by looking at the set of ordered pairs that are presented in this mapping. Specifically, we can tell this because of none of the x-values repeat: (1,1), (1,1), (7,49), (0.5, 0.25). (It is important to keep in mind that although if the output value of 1 can be repeated, the input values cannot.)
The inverse functions of trigonometry have the following domains and ranges:
The input is called the domain, and the output is called the range.
When dealing with inverse functions, X is input, and angle is output.

Therefore, the domain consists of all the possible values of x, while the range comprises all the possible angles.
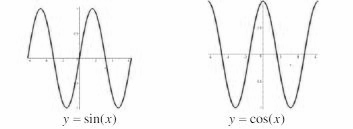
Both the sine and cosine functions have their own domains and ranges.
Since the domains of the sine and cosine functions are not constrained in any way, we can say that their domains are such that x is greater than R. It is important to note, however, that the range for y = sin(x) and y = cos(x) is the same: between -1 and 1. Therefore, alterations made to these functions in the form of shifts and stretches will have an effect on the range but will not have any effect on the domain.

The domain and range for tangent functions
Notice that y = tan(x) has vertical asymptotes at (2n+1)2 . Therefore, its domain is such that x(2n+1)2 . However, because the function can take on any value for y, its range is specified as being between y and R. In this particular scenario, transformations will have an impact on the domain but will have no effect on the range.

Find the domain and range of the function y = cos(x) – 3 as an example.
Solution:
Domain: x ∈ R
Range: – 4 < y ≤ – 2, y ∈ R
Take note that the range has just been moved downward by three units.
Domain and Range of Sin(x)
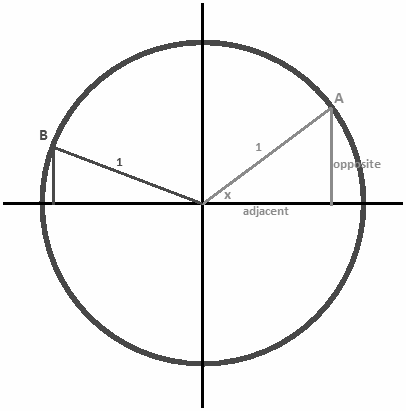
Imagine a circle with a radius of one and its centre at the origin. This will help us determine the domain and range of the sin(x) function. If we construct a triangle with a right angle from any point on this circle, the hypotenuse of that triangle will always equal 1. Similar to this:
|
According to what we know, the value of sin(x) can be expressed as the opposite value divided by the hypotenuse. At any point in this unit circle, the value of sin(x) is equal to the opposite divided by 1. This opposite measure can be constructed for each and every point on the circle, which indicates that the angle x can be any value at all. Therefore, the territory covered by sin(x) includes all of the real numbers.
In addition, the value of sin(x), which varies according to the point on the circle that is being considered, can reach a maximum of 1 when x is equal to 90 degrees and a minimum of -1 when x is equal to 270 degrees. Therefore, the value of sin(x) can be anywhere from -1 to 1.
To summarise, the following is the solution for y = sin(x):
Domain = [+ ∞, – ∞]
Range = [-1, +1]
Conclusion
In most cases, we find the domain by looking for those values of the independent variable (often x) that we are permitted to use. This is how we establish the boundaries of the domain. (It is imperative that we steer clear of writing 0 at the end of a fraction or negative numbers beneath the square root sign.)
After plugging in the various possible x-values, we may determine the range by determining the y-values that are produced as a result.