The dimensional analysis provides solutions to several intriguing topics. Is one second or one metre longer? Is it possible to compare the two? Is it possible to multiply a kilogram by 12 eggs? Correct? After studying this part, you will be able to grasp how dimensional analysis solves these problems. Start now!
Introduction
The use of dimensions and the dimensional formula of physical quantities to uncover interrelationships between them is known as dimensional analysis. Because we utilise conversion factors to get the same units, dimensional analysis is also known as the factor label method or unit factor method.
Definition
The dimensional analysis uses a set of units to determine the form of an equation or, more commonly, to ensure that the result of a computation is correct as a safeguard against many common errors.
The units included are:
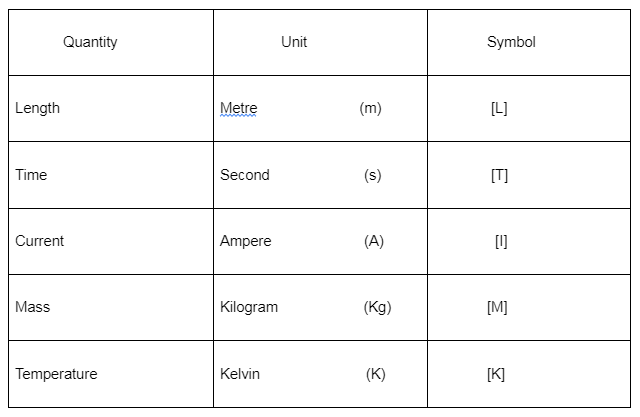
These units are also known as SI measurement system base units. Base units are used to measure light intensity and material amount.
Only one combination of the units above can measure all quantities. Density, for example, is measured in Kg/m3.
We would write this as [M]/[L3] or [M L-3] in dimensional symbols.
Homogeneity principle
The principle of Homogeneity stipulates that the dimensions of each term in a dimensional equation should be the same on both sides. This idea is useful since it allows us to translate units across different forms.
Factor labelling using dimensional analysis
It is possible to convert units between different measurement systems. Factor label technique, unit factor method, or dimensional analysis are used to describe this approach.
Conversion factors are used to express the connection between different systems’ units, making it possible to move an item from one to another. Based on the fact that the ratio of each basic quantity in one unit with their counterpart in another unit is equal to one, the formula is used.
For instance,
1) How many hours and minutes are in a day?
Solution:
60 minutes is equal to one hour. Three hours equals 180 minutes.
We use conversion factors to ensure that the answer is correct and that conversion factors do not skew the results. The conversion factor is used to change the unit system of each basic quantity, such as mass, length, and time.
Application of dimensional analysis
In real-life physics, dimensional analysis is a crucial part of the measurement. We use dimensional analysis for three main reasons:
- To ensure that a dimensional equation is consistent.
- Determining the relationship between physical quantities in physical phenomena
- To switch from one system to another’s units
- Development of a fluid phenomena equation
- The number of variables necessary in an equation is reduced.
Dimensional analysis’s drawbacks and pitfalls
Dimensional analysis has several drawbacks, such as that it can only be used in certain situations. Because numerous physical quantities have the same dimensions, the uniqueness of physical quantities does not rely on their dimensional formulas.
Using the dimensions technique, a formula involving more than three physical quantities cannot be derived.
Summary
Dimensional analysis is a fantastic technique to examine the relationships between physical quantities. Because only two quantities of the same dimension may be added, subtracted, or compared, this is the principle of homogeneity.
If we know what kinds of quantities are involved, we may utilise dimensional analysis to build credible equations.
Conclusion
A dimensional equation’s correctness can be checked via dimensional analysis to determine how physical quantities in physical phenomena relate to each other. Dimensional analysis is the process of determining the dimensions and units of measurement of various physical quantities to determine how they relate to one another. While this may be true, it is only feasible to do a dimensional analysis if all sides of an equation have identical dimensions. The concept of uniformity of dimensions governs this. Only quantities of the same dimension may be added, subtracted, or compared.
In addition, dimensional analysis is a fantastic tool for determining whether or not an equation is dimensionally accurate. Dimensional analysis may also develop reasonable equations if the quantities involved are known. Dimensional analysis may be used to determine the size and form of objects. Dimensional analysis has made it feasible to conduct research into the nature of things mathematically.
Most physical quantities can already be expressed in terms of fundamental dimensions. Dimensional analysis and its applications may now be studied using basic variables such as mass, time and distance.