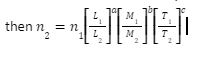

The powers to which the fundamental units are elevated to obtain one unit of a physical quantity are called the dimensions of that quantity.
While writing any dimension we will observe that it has two parts, the first part is a numerical value that expresses the magnitude of the dimension and the second part is the unit such as length, mass or time.
While writing the mass of any object we write as 60 kg or 1000 g. This kg and g denote that the numerical value written before it is the magnitude of mass.
Fundamental and derived quantities:
Fundamental quantities are quantities that are not dependent on other quantities. Essential units are the units that are used to measure these fundamental quantities. C.G.S., M.K.S., F.P.S., and SI are the four systems of units.
Example: – centimetre, gram, second.
The derived quantities are those that are derived from the basic quantities. Derived units are the units that are used to measure these derived quantities.
Example: – newton(N), Pascal (Pa), Hertz (Hz).
Dimensional Analysis
Dimensional analysis is founded on the idea that two quantities with the same dimensions can only be compared. Because they have the same dimension, we may compare kinetic and potential energy and claim they are equal or one is bigger than the other. However, because their dimensions aren’t the same, we can’t relate kinetic energy to force or acceleration.
Dimensional analysis can also be used to figure out how two or more physical quantities are related. We can utilise the principle of consistency of two expressions to determine the equation linking these two values if we know the degree of reliance of one physical quantity on another, that is, the degree to which one quantity changes with a change in another.
Dimensional formula
The dimensional formula of a derived quantity is an equation that shows the powers to which the fundamental units must be increased to acquire one unit of that quantity.
Let us assume a quantity P that is derived by P=MaLbTc in this quantity, MaLbTc is known as the dimensional formula and a, b and c is called the dimension.
Dimensional constants
Dimensional constants are physical values that have dimensions and have a fixed value. Examples include the gravitational constant (G), Planck’s constant (h), Universal gas constant (R), and the speed of light in a vacuum (C).
Law of homogeneity of dimensions
- In any correct equation representing the relation between physical quantities, the dimensions of all the terms must be the same on both sides. Terms separated by ‘+’ or ‘–’ must have the same dimensions.
- A physical quantity Q has dimensions a, b and c in length (L), mass (M) and time (T), respectively and n1 is its numerical value in a system in which the fundamental units are L1, M1 and T1 and n2 is the numerical value in another system in which the fundamental units are L2, M2 and T2, respectively
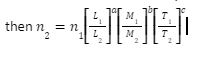
Limitations:
This approach is incapable of determining dimensionless quantities. This approach cannot calculate the proportionality constant. They can be discovered by experiment (or) theory.
Trigonometric, logarithmic, and exponential functions are not relevant to this approach.
This strategy will be difficult to use when physical quantities are reliant on more than three physical qualities.
In some circumstances, the constant of proportionality also possesses dimensions. We are unable to use this system in such circumstances.
We cannot use this method to get the expression if one side of the equation comprises addition or subtraction of physical quantities.
Dimensional consistency:
Because only physical quantities with equal dimensions can be added or removed, two quantities of different dimensions cannot be combined together. We can’t combine mass and force, or electric potential with resistance.
The principle of homogeneity of dimensions is used to assess the equation’s accuracy and consistency for any given equation. If the dimensions of each component on either side of the sign of equality are not the same, the equation is deemed incorrect.
Applications:
When working with physical quantities, dimensional analysis is critical.
The foundations of dimensional analysis were laid by Fourier. The dimensional formulas are used to do the following:
- To Check if a physical equation is correct.
- To Determine a physical quantity’s relationship.
- The conversion of a physical quantity’s units from one system to another.
Important physical constants:

Conclusion
A unit is a universally recognised unit of measurement for measuring quantities. A numeric quantity and a specified unit have been provided in the measurement. Fundamental units are used to specify base quantities (such as length, mass, and so on). The units that are derived from fundamental units are known as derived units. A System of Units is made up of both fundamental and derived units.