The trigonometric function ‘Cosine’ is abbreviated as Cos. The ratio of the length of a right-angle triangle’s base to its hypotenuse is known as cosine (the longest and slant side). Where x is the angle between the two sides, cos (x) = basehypotenuse=bh
For cos 300 There are three basic values. As previously mentioned, the value of a trigonometric ratio is in fractional form equal to 32. The value of cos 30 in the circulatory system, employing trigonometric functions in the cartesian plane, is pi/6 or 180/6. Although this is the specific solution to one cycle, if n cycles are present, the result becomes (n x pi / 6). The centesimal system, which yields (1/3) g, cos 33 is the final method for calculating the value of cos 30. Regardless of the method used, the decimal value of cos 30 is always 0.8660254037.
The decimal value of cos 45 degrees is 0.707106781. The equivalent of the given angle (45 degrees) in radians can also be used to express Cos 45 degrees (0.78539 . . .)
Using the degree to radian conversion, we know that in radians = in degrees (pi/180°) 45 degrees = 45 degrees = 45° × (π/180°) rad = π/4 or 0.7853 . . .
∴ cos 45° = cos(0.7853) = 1/√2 or 0.7071
In units of trigonometric functions, cos 300 and cos 450
We may represent the cos 300 degrees using trigonometric formulas as:
- (1-(300)
- 11+(30°)
- cot 30° 1+(30°)
- 30°-1 csc 30°
- 1sec 30°
For cos 450 using trigonometric formulas as:
- (1-(450)
- 11+(45°)
- cot 45° 1+(45°)
- 45°-1 csc 45°
- 1sec 45°
To represent cos 30° as trigonometric identities
- –cos 180°-30°=-cos 150°
- –cos 180°+30°=-cos 210°
- sin 90°+30°=sin 120°
- sin 90°-30°=sin 60°
To represent cos 450 as trigonometric identities
- –cos 180°-45°=-cos 135°
- –cos 180°+45°=-cos 225°
- sin 90°+45°=sin 135°
- sin 90°-45°=sin 45°
How to find cos 300
In the first quadrant, the cosine function is positive. The cos 300 value is given as 0.86602…. The value of cos 30 degrees and can be found by:
- Using Unit Circle
- Using Trigonometric Functions
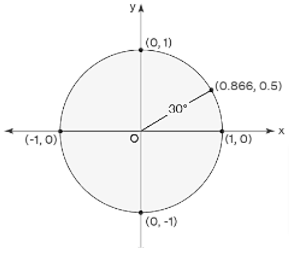
Using a Unit Circle, calculate Cos 30 degrees

Figure 1
Using the unit circle, find the value of cos 30 degrees:
Anticlockwise rotate ‘r’ to produce a 30° angle with the positive x-axis.
x-coordinates (0.866) Of the point of intersection (0.866, 0.5) of the unit circle and r equals the cos of 30 degrees.
As a result,
cos 30° = x = 0.866. (Approx)
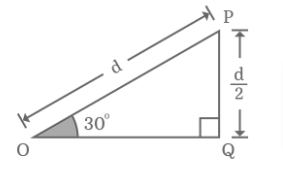
Using Trigonometric Functions

Figure: 2
In trigonometry, the cos ( 3313) squared identity is used to evaluate value.
6) is actually calculate by substituting the value of sin 30 degrees in this formula.
cos 300=1-(300)
cos 300=1-(12)2
cos 300=1-14
cos 300=1×4-14
cos 300=4-14
cos 300=34
cos 300=32
Methods for Determining the Cos 45 Degrees Value
In the first quadrant, the cosine function is positive. The cos 450 value is provided as 0.70710…. The value of cos 45 degrees can be found by
- Using Unit Circle
- Using Trigonometric Functions
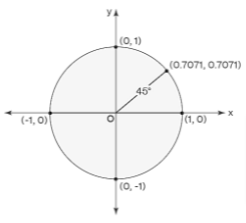
Using a Unit Circle, calculate the cosine of cos 450

Figure: 3
Using the unit circle, find the value of cos 450 :
Anticlockwise rotate ‘r’ to produce a 45° angle with the positive x-axis.
The x-coordinate (0.7071) of the point of intersection (0.7071, 0.7071) of the unit circle and r equals the cos of 45 degrees.
As a result,
cos 450=x= 0.7071 . (Approx)
Using Trigonometric Functions
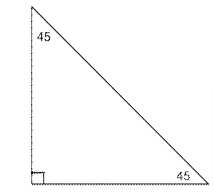
Only when you have a right triangle can you perform trigonometric functions directly on it. As in, if you just “take the cosine” of an angle, the angle must be in a right triangle.
We have, 1800–900–450=450
As a result, your three angles are 450,450, 900

Figure: 4
if you draw a line from the bottom left corner of this triangle to the middle of the hypotenuse, you’ve constructed a symmetry line and that these two legs are identical. It isn’t a 45-45-90 right triangle if you can’t.
Now, use Pythagorean Theorem for determining the length of either of those legs:
a2+b2=c2
a=b
a2+b2=c2
2a2=12=12
a2=12
a=12=12
Because it is usual to avoid using a square root in the denominator of a calculation:
a=12.22=22
As a result, each of those two legs is 22 units long. Because cos is “adjacent over hypotenuse,” taking the cos of any of two 450 angles gives you:
cos 450=221 =22
Examples of cos 300 and cos 450
- If sec 30° is 1.1547, what is the value of cos 30°?
Solution: cos 30° = 1/sec 30°
⇒ cos 30° = 1/1.1547 = 0.866
- Stated the following: 5 (cos 45°/sin 135°)
Solution:
As we know cos 450 = sin 135°
5 cos 45°/sin 135° = 5 (cos 45°/cos 45°)
= 51= 5
Conclusion
The cosine function is a periodic function that is extremely important in trigonometry, as we will see in this article. The simplest way to understand the cosine function is to use the unit circle. Draw a unit circle on the coordinate plane and, for a given angle measure, draw the angle centered at the origin, with one side as the positive x-axis. Because secant is the reciprocal of cosine, the secant of any angle x for which cos x=0 should be unknown because the denominator would be zero. The secant of (pi)/2 must be undefined because cos (pi/2) has a value of 0. To find out the value of different methods used.