Generally speaking, a function is a specific relationship between two sets in mathematics (input set and output set). There is a unique relationship between every member of the output set and one or more members of the input set. The function is denoted by the letter “f.” It is possible to have multiple types of functions. They are organised into groups based on their categories. One of these categories is the graph’s inherent character. In accordance with the nature of the graph, it is possible to classify the functions into two types:
•Convex Function
•Concave Function
Both the concavity and the convexity of a function can occur once or more than once in the same function. Alternatively, inflection point or point of inflection refers to the location where the function is neither concave nor convex at any given position. In this article, the concept and significance of the inflection point, as well as how to graphically determine the inflection point, are discussed in detail in depth.
Definition of an Inflection Point
It is the point of inflection, also known as the inflection point, where the concavity of the function changes. It signifies that the function changes from concave down to concave up, or vice versa, depending on the direction of the arrow. In other terms, an inflection point is the point at which the rate of change of slope changes from increasing to decreasing, or vice versa, is known as a tipping point. Those points are not, by any means, local maximum or minimum points. They are considered to be stationary spots.
Concavity Function
In most cases, when the curve of a function bends, it takes on the shape of a concave cylinder. The concavity of a function is the term used to describe this phenomenon. There are two types of concavity that can be detected in a graph function.
•Concave up
•Concave down
An upward-opening curve, or a curve that bends up into the shape of a cup, is said to be concave up or convex down, depending on which direction the curve opens or bends.
Curves that are concave down or convex up are characterised by the fact that they bend down or resemble a cap in shape. In other words, if the slope of the tangent increases as a result of an increase in an independent variable, the tangent sits beneath the curve and vice versa.
Calculus of Inflection Points
It is considered to be a differentiable function if f(x) has the following form:
•Concave up a point x = a, iff f “(x) > 0 at a
•Concave down at a point x = a, iff f “(x) < 0 at a
f “(x) is the second order derivative of the function f(x).
Inflection point graph
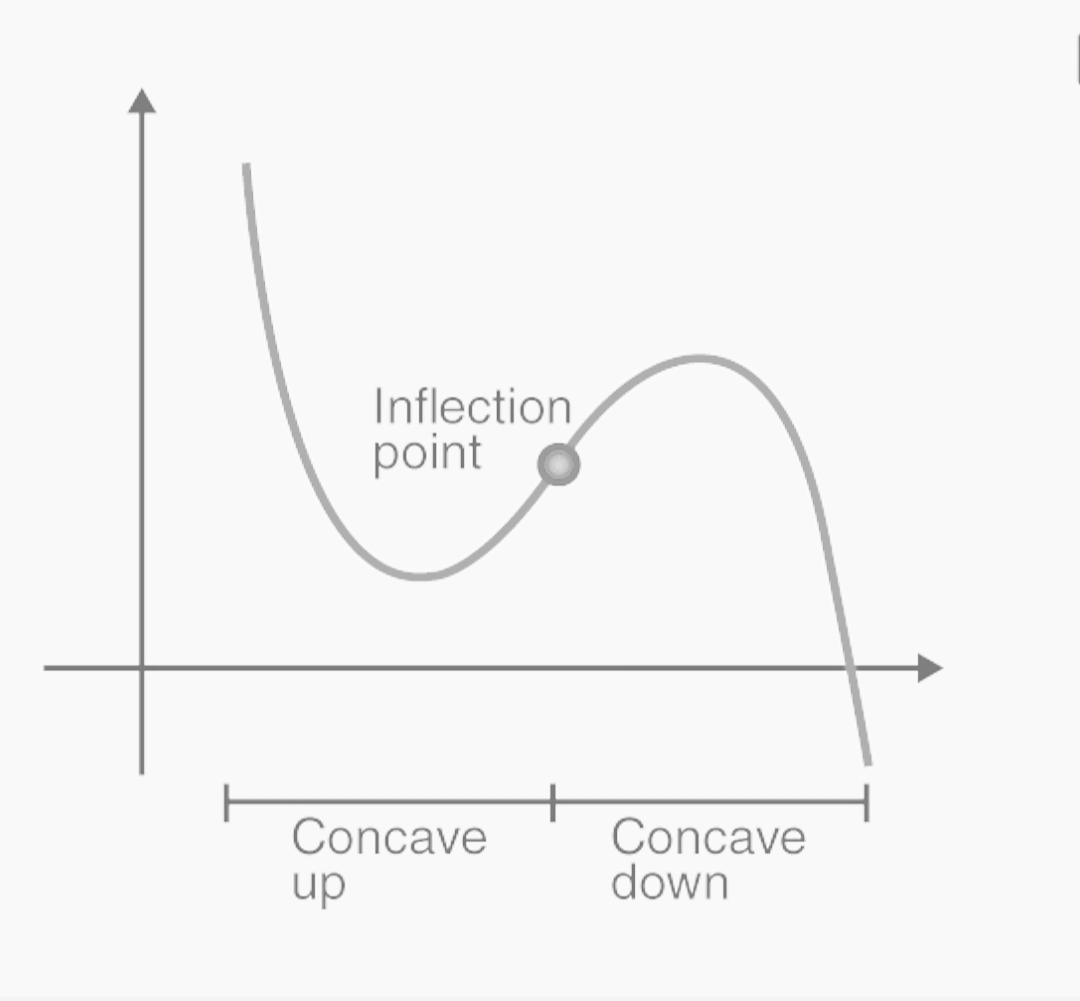
A point of inflection is a graphing point that specifies the slope of a graph of a function where the particular point is equal to zero. The inflection point of the function is depicted in the graph to the right.
It should be noted that there can be more than one point of inflection in a single curve or within a particular interval of a function inside a single curve.
Finding inflection Point on a Graph
An inflection point on a curve is defined as a point on the curve when the concavity of the curve shifts. The sign of the curvature changes, in other words. The function is concave up when f “> 0, and it is concave down when the value of f ” <0, as we already know. Whenever the value of the function moves from positive to positive, or from negative to positive, at the position x = c on a graph, that point is referred to as the point of inflection.
A function’s inflection point
It is possible to determine the inflection point of a function based on the sign of the second derivative of the function being considered. Point inflection can also be classified into two categories based on the value of the first-order derivative of the function, as shown in the diagram below.
If the value of f'(x) is zero, the point is said to be a stationary point of inflection.
As long as the function f'(x) does not equal zero, the point is considered a non-stationary point of inflection.
Conclusion
A function is a specific relationship between two sets in mathematics (input set and output set). There is a unique relationship between every member of the output set and one or more members of the input set. The function is denoted by the letter “f.”Both the concavity and the convexity of a function can occur once or more than once in the same function. Alternatively, inflection point or point of inflection refers to the location where the function is neither concave nor convex at any given position.It is the point of inflection, also known as the inflection point, where the concavity of the function changes. It signifies that the function changes from concave down to concave up, or vice versa, depending on the direction of the arrow.It is possible to determine the inflection point of a function based on the sign of the second derivative of the function being considered.