
A function is what relates an input with the output. It relates the individual elements of a set to the individual elements of another set. Functions are the fundamental concept in Mathematics. We apply it almost everywhere. These functions play a vital role in the modelling of every new structure, machine, or automobile.
For learning about the codomain of relations, we need to understand relations. Now, a collection of all ordered pairs (a,b) is the Cartesian product of two sets, A and B, such that a∈A and b∈B. A subset of this Cartesian product is called a relation. So we can say that it is a rule that relates elements of one set to the elements of another set. A function is a special kind of relation.
Also, in the function g(x) = x2, the range of different domains can be the same. In the stated example, g(-1) = 1 and g(1) = 1 as well. Whereas the answers for f(x) are always the same. In simple mathematics, the domain is usually assumed.

Codomain of relations
Domain
A domain is all the values that go into a function. It is an essential part of a function. A function can entirely change if we change its domain. Let us take an example of a simple function like f(x) = x2. This function can have the domain (what goes in) of just the counting numbers {1,2,3,…}, and the range will then be the set {1,4,9,…}. On the other hand, a function g(x) = x2 can have the domain of integer {…,-3,-2,-1,0,1,2,3,…}, in which case the range is the set {0,1,4,9,…}. Here the domain of both the functions is different, so the range is also different.Also, in the function g(x) = x2, the range of different domains can be the same. In the stated example, g(-1) = 1 and g(1) = 1 as well. Whereas the answers for f(x) are always the same. In simple mathematics, the domain is usually assumed.
Codomain
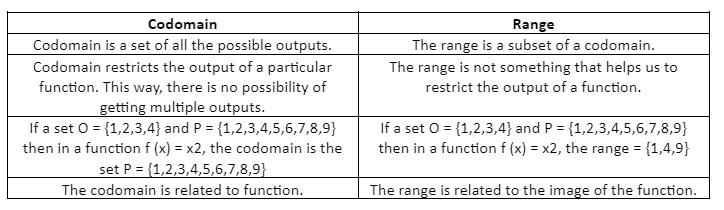
Codomain is the set of all the possible outputs in a function. To simplify, what goes in the function is the domain, and the codomain can come out of the function. When we use the function notation f: R 🡪 R, we mean the codomain of f is the set of real numbers R. For example, set A = {1,2,3,4} and set B = {1,2,3,4,5,6,7,8,9,10}. Now, for a function f(x) = 2x+1, The codomain will be {1,2,3,4,5,6,7,8,9,10}. Have a look at the codomains of some frequently used functions while solving mathematical problems in the table given below:
Importance of codomain
Choosing the correct set as codomain is very important. It helps us consider whether something is a set or not. A function should be single-valued and not have multiple results for the same unit. If we assume codomains to be real numbers, then the square root ceases to function. For instance, f(25) = 5 or -5. In this case, square root cannot be considered a function as there are multiple outputs—the reason is the selection of real numbers as the codomain. This is why codomain is important. One can avoid the error provided in the explanation by choosing the correct codomain. In this case, the codomain should be limited to positive real numbers. S basically, the nature of codomain is to restrict the output of a given function.Relation of codomain with range
As stated earlier, the codomain is the set of outputs in a function. So we can say that range is a subset of codomain. Another thing to remember is that the range and codomain can be equal in some cases, but the range can never be greater than the codomain. Let us draw a comparison between the codomain and the range of a function.