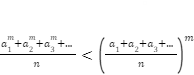
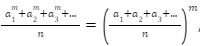
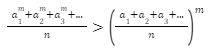
An observation can be based upon any test or experiment. The changes in the value can vary between a range. The value for each experiment may not be identical and are usually within a range of numbers. This range may not be useful in all scenarios to denote a common value.
An observation can be any set of values in the statistical domain, regardless of the experiment. It can be the height of people, marks of students, or sales value per month. It becomes abruptly challenging to get all the values and note them. Missing out values can become a serious issue. This is why a unique value representing the overall observation is required. Hence, it is vital to find the arithmetic mean of a series.
The arithmetic mean was introduced as a value representing the overall data for the taken observation.
What is the Importance of Arithmetic Mean in an Observation?
Assume that a sample experiment takes place such that the observed values are in a given range. Suppose a total of m readings were noted and analysed. The readings can have different values, wherein a few might repeat. Now, the term denotes the overall experiment as a whole. Thus, we can find the mean for the whole lot to represent it.
What is mean? A simple question arises at this point. The answer to this question is the overall representation of data. The mean is computed from data by taking the average for each entry to the exact value. The mean can be called the mid-value, such that the total deviation is tending to zero from this unique represented value for the overall data. The calculation for this is similar to finding out the average for any set of values for any test.
When we find the average, we initially observe the values we have from the experiment. These values can be added together to get a single value. The summation of the observation is considered for finding out the mean to represent as a whole. This value is then divided by the total number of observed values to get the average value for the experiment. This value represents the whole lot uniquely and is the mean for any given data. The arithmetic mean represents the mean for the given arithmetic observation.
The arithmetic mean can be evaluated for different series of mth power wherein different cases are taken into consideration. The unique value of power leads to different cases. For example:
For an individual series, the experiment had m readings, and the values can be unique or repeating depending on the type of experiment we had. Suppose, the different values are a1, a2, a3…. and so on. The total observations are n.
Now, the mean will represent the overall data from the experiment carried out.
Thus, one can say that, if the mth power lies between 0 and 1, i.e. m (0,1), then
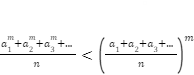
For a series, if the mth power is either 0 or 1 with the boundary included, i.e. m {0,1}, then we can say that,
![]()
For a series, if the mth power is any real value except lying between 0 and 1 with the boundary included, i.e. m R-[0,1], then we can say that,
![]()
Hence, depending on the mth power, we can compute the mean of the given series for any experiment.
These formulas can be used on any set of observations for a sample experiment. Statistics use this in different domains to carry out the representation of the central tendency. This is way far the most prominent formula for evaluating a value to represent the overall experiment as a whole.
Conclusion
The arithmetic mean of a series or of different observations for any set of tests or experiments can be used to represent the whole as a one valued observation. This value can be part of the experimental observations or a unique value for the experiment. Depending on the number and value of the observations, the mean can have different values. Note that, if we add or subtract a value from the observation, the mean value deviates from the computed value.