Any angle can be used to span overlapping lines. This angle is always less than 180°and larger than 0°. Vertical angles are formed by intersecting two lines. Vertical angles have a shared vertex and are opposite angles (which is the point of intersection).
Meaning of intersection of two lines
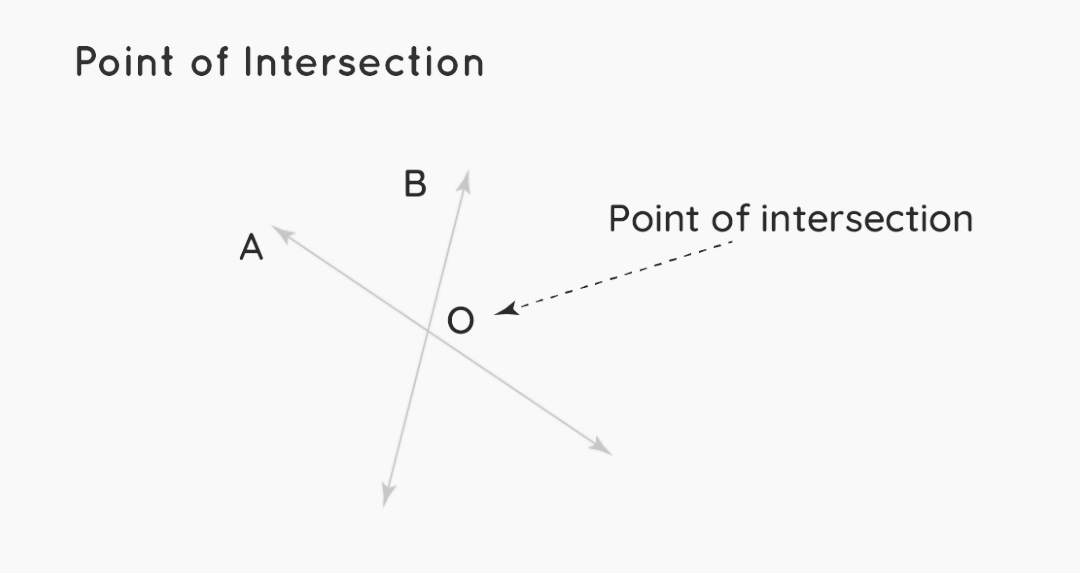
The relationship between two lines that share exactly one point is referred to as “intersecting lines,” and the word “intersecting lines” refers to this relationship. Both of the lines that cross at the same point share a single point in common. The point at which all of the lines that intersect with one another share a point in common is known as the point of intersection of those lines. When two co-planar straight lines that are not parallel to one another meet, they will meet at a location that is designated as the point of intersection. It is said to be the point of intersection when lines A and B meet at point O. This point serves as the intersection of the two lines.

Finding the point where two lines intersect
Let’s have a look at the following possible outcome, shall we? We have been given two lines, L1 and L2, and we are to find the point where they intersect. The instructions for this task have been provided to us. In order to calculate the value of the point of intersection, it is necessary to find a solution to two linear equations that can be solved simultaneously.
Let us set out the equations that describe the two lines in a general manner as follows:
a1x + b1y + c1 = 0
a2x + b2y + c2= 0

For the time being, let’s assume that the point of intersection is located at (x0, y0). Thus,
a1x0 + b1y0 + c1 = 0
a2x0 + b2y0+ c2 = 0
By using Cramer’s rule to this system, one can accomplish the following and acquire the desired results:
x0/(b1c2-b2c1) = -y0/(a1c2-a2c1)= 1/(a1b2-a2b1)
With the use of this connection, we are able to determine the coordinates of the point of intersection (x0, y0), which tells us that it is as follows:
(x0,y0) ={(b1c2-b2c1)/(a1b2-a2b1),(c1a2-c2a1)/(a1b2-a2b1)}
The angle of intersection
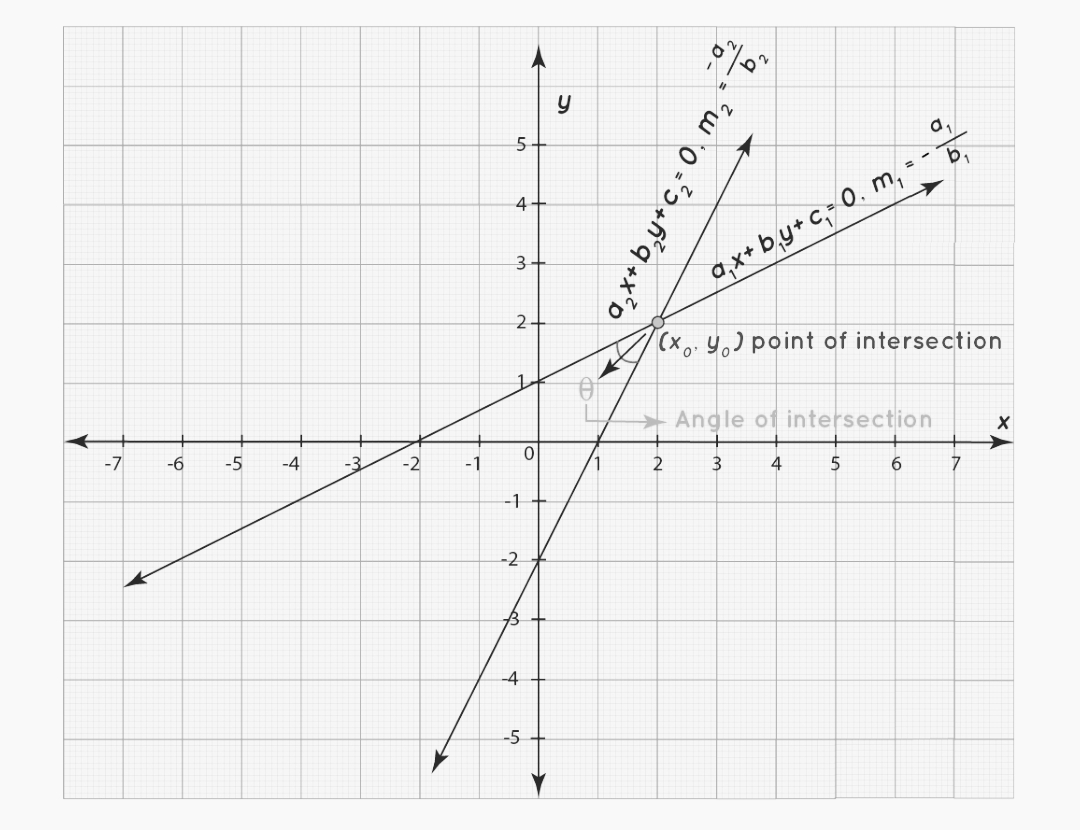
Consider the figure that follows in order to calculate the angle formed by the intersection of two lines:
The slope-intercept form of the equations for the two lines is as follows:
y= -(a1/b1)x +(c1/b1) =m1x+c1
y= -(a1/b1)x +(c2/b2) =m2x+c2
Take note in the preceding picture that equals θ=θ2-θ1 , and that as a result,
tanθ=tan(θ2-θ1)=
(tanθ2-tanθ1)/(1+tanθ2tanθ1)
= (m2-m1)/(1+m2m1)
Traditionally, we would only be concerned in the acute angle that exists between the two lines; as a consequence, we require tan to be a quantity that has a value that is greater than zero.
Therefore, in the expression that was just discussed, if the expression (m2-m1)/(1+m2m1) ends up having a negative value, this would be the tangent of the acute angle that exists between the two lines. Obtuse angles are formed when two lines intersect at an acute angle. The magnitude of this expression will be utilised, as a result, in the process of determining the size of the acute angle that may be found between the two lines.
As a consequence of this, the acute angle that is formed by the intersection of the two lines is.
θ=tan-1|(m2-m1)/(1+m2m1)|
As a result of this relation, deriving the requirements that must be satisfied by m1 and m2 in order for the two lines L1 and L2 to be either parallel to one another or perpendicular to one another is a simple and straightforward process.
The factors that determine whether two lines are parallel or perpendicular to one another
•Because the slope of parallel lines must always be the same, it shouldn’t come as much of a surprise that if the lines are parallel, then θ= 0 and m1 = m2, as the slope of parallel lines must always be the same.
•In order for the two lines to be considered perpendicular to one another, it is necessary that, = π/2. This ensures that cotθ= 0 at all times. This is a possibility in the event that 1 + m1m2 = 0 or if m1m2 = 1.
•If lines L1 and L2 have the general form ax+ by + c = 0, then the slope of this line may be computed using the formula m = -a/b.
•The necessary condition for achieving parallelism in the progression of two lines
Therefore, in order for L1 and L2 to be parallel, the following requirements need to be met for both languages:
m1=m2=⇒-a1/b1 = -a1/b2 ⇒a1/b1 = a2/b2
•The condition that must exist for two lines to be perpendicular to one another.
In order for L1 and L2 to be in a perpendicular connection, the following conditions need to be met:
m1m2=-1 ⇒(-a1/b1)(-a1/b2) =-1
⇒a1a2+b1b2=0
Conclusion
There is a maximum of one point of junction that can be located at the intersection of two distinct lines. The general form of the two equations, which is represented by the notation a1x + b1y + c1= 0 and a2x + b2y + c2= 0 correspondingly, is required in order to locate the point at where two lines intersect in order to determine where the point of intersection is. Only in the case when the lines are not perpendicular to one another will they come into contact with one another. The relationship between two lines that share exactly one point is referred to as “intersecting lines,” and the word “intersecting lines” refers to this relationship. Both of the lines that cross at the same point share a single point in common. The point at which all of the lines that intersect with one another share a point in common is known as the point of intersection of those lines. Because the slope of parallel lines must always be the same, it shouldn’t come as much of a surprise that if the lines are parallel, then θ= 0 and m1 = m2, as the slope of parallel lines must always be the same.