The cubic (or isometric) crystal system is a crystal system in crystallography in which the unit cell is shaped like a cube. This is a very common and straightforward shape found in crystals and minerals.
These crystals are classified into three distinct types:
- Cubic primitive (alternatively called simple cubic)
- Cube with a body-centered center (abbreviated bcc)
- Cube with a face-centered center (abbreviated fcc, and alternatively called cubic close-packed or ccp).
While the unit cell in these crystals is frequently assumed to be a cube, the fundamental unit cell is frequently not. The term “body-centered cubic” (BCC) refers to a particular sort of atom arrangement found in nature. A body-centered cubic unit cell structure is composed of atoms organized in a cube with one atom in each corner and one atom in the center.
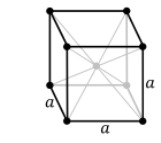
Eight other unit cells share the atom at the cube’s corners. As a result, each corner atom is one-eighth of an atom in size. As a result, the BCC structure is considered to have an eight-coordinate structure.
Because the unit cell’s center contains one complete atom, the total number of atoms in the BCC unit cell structure is two: one in the center and eight one-eighth atoms at the corners.
1 atom + (1/8 atoms x 8 corners) = 2 atoms
The BCC unit cell structure does not compact the atoms as tightly as other configurations (such as the face-centered cubic, FCC). However, the configuration of the atoms makes it more difficult for them to pass through one another. This property renders BCC formations more difficult to work with and less pliable than densely packed materials such as gold. This may be critical when it comes to material selection for specific applications.
Metal atoms naturally crowd together to produce the strongest metallic link possible. Numerous packing patterns are present in nature, including the body-centered cubic (BCC) configuration.
The directions in which the atoms touch is one of the fundamental characteristics of BCC. Along the cube’s edges, the atoms do not touch. Rather than that, the atoms make contact along the cube’s diagonal. In other words, the core atom is in contact with every corner atom.
In addition to the eight corner points, the body-centered cubic system has one lattice point in the middle of the unit cell. Each unit cell contains a total of two lattice points.
Density of Packing in the Body-Centered Cubic
Packing density is another characteristic that is used to define the BCC structure. The packing density, alternatively referred to as the atomic packing factor (APF), is essentially the fraction of a crystal structure’s volume occupied by atoms.
The APF of a BCC structure is equal to the volume of the unit cell’s atoms divided by the unit cell’s volume.
Therefore:
APFBCC = Vatoms/Vunit sphere
Voids within the unit cell
Voids are also referred to as interstitial sites or holes within the unit cell. They are the vacant space between the atoms’ (spheres’) packing in unit cells.
If you attempt to cluster circles together, the holes are easily visible. No matter how close they are or how they are arranged, there will remain empty spaces between them. The same is true in a unit cell; regardless of how the atoms are arranged, interstitial spaces will exist between them. Other atoms can be used to fill these spots or holes. The illustration with packed circles is simply a two-dimensional representation. The atoms (spheres) in a crystal lattice would be packed in a three-dimensional pattern. This leads to a variety of various-shaped interstitial sites depending on the lattice arrangement of the atoms.
Six octahedral voids are situated in the middle of each face of a body-centered cubic unit cell, and twelve more ones are located at the midway of each cell’s edge, for a total of six net octahedral voids. Additionally, there are 24 tetrahedral voids distributed evenly around each octahedral void, totalling twelve net tetrahedral voids. While these tetrahedral voids are not truly voids, they do occasionally arise in multi-atom unit cells.
CONCLUSION-
The body-centered cubic (BCC) unit cell is a third typical packing configuration in metals. It contains atoms at each of the cube’s eight corners plus one atom in the cube’s center. Due to the fact that each corner atom is a corner of another cube, the corner atoms in each unit cell are shared between eight unit cells.
The Body-Centered Cubic (BCC) crystal structure is significant because it is exceedingly frequent in metals and results in interesting features such as a high ductile-to-brittle transformation temperature (DBTT).
BCC is a nearly densely packed material with an APF of 0.68. Numerous features develop as a result of the fact that the next-nearest neighbours bond almost as strongly as the nearest neighbours.