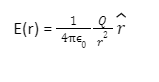
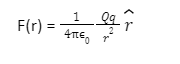
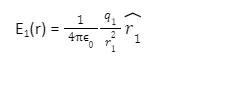
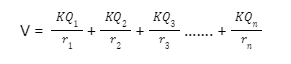
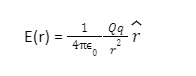
The electric potential is a metric for how much energy is stored per unit of charge.
Electric potential energy is the amount of energy gained when an object moves against an electric field. For each charge, the electric potential is determined by dividing the potential energy by the charge quantity.
For a uniform field, the relationship between the electric field (E), the potential difference between points A and B (ϕ), and the distance between points A and B (d) is:
E =ΔΦ − d
The magnitude of the electric field E created by a point charge Q is E = K|Q|/r2
The electric field is a vector field that can be associated with any place in space and indicates the effort per unit charge produced on a positive test charge that is at rest at that location.
The electric field is created by the electric charge or by magnetic fields that change over time. The electric field is responsible for the attraction forces that hold the atomic nucleus and electrons together at the atomic scale.
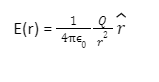 Where r is a unit vector from the origin to r, as a result, for each value of the position vector r, the above statement provides the electric field value.
The presence of an electric field due to a point charge is related to the action of a charge.
The force F that a charge Q exerts on another charge q is computed as:
Where r is a unit vector from the origin to r, as a result, for each value of the position vector r, the above statement provides the electric field value.
The presence of an electric field due to a point charge is related to the action of a charge.
The force F that a charge Q exerts on another charge q is computed as:
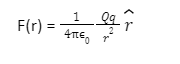 If the charge q is symbolised by the vector r, it feels a force F equal to the charge q multiplied by the electric field E at the location of q.
As a result, F(r) = q x E(r)
If the charge q is symbolised by the vector r, it feels a force F equal to the charge q multiplied by the electric field E at the location of q.
As a result, F(r) = q x E(r)
The electric field E1 caused by q1 at r1 is expressed as,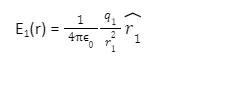 Here r1 is the distance between q1 and P, and r1 is the unit vector in the direction from q1 to P.
Here r1 is the distance between q1 and P, and r1 is the unit vector in the direction from q1 to P.
In the same way, the electric field E2 cause by q2 at r2 can be written as,
Here r2 is the distance between q2 and P and r2 is the unit vector in the direction from q2 to P. Charges q3., q4…, qn cause similar expressions for fields E3, E4…, En . The electric field E due to the system of charges can be represented as follows using the superposition principle:
E(r) = E1 + E2 + E3 …………+ En . ( All in vector form )
The source charge positions determine E, which is a vector variable that varies from one location in space to another.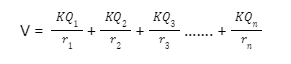
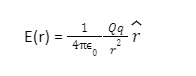 The amount of work energy necessary to shift a unit of electric charge from a reference point to a specific place in an electric field is known as electric potential energy.
The amount of work energy necessary to shift a unit of electric charge from a reference point to a specific place in an electric field is known as electric potential energy.
Electric Field due to a point charge
Faraday was the first to introduce the concept of the field. The strength of the electric field due to a point charge is the electric field intensity at that point. Consider a point charge Q that is kept in a vacuum at the origin O. According to Coulomb’s law, if another point charge q is kept at a position P from the charge Q, where OP = r, the charge Q will create an electrostatic force on q. The charge Q creates an electric field that acts all around the place. The field at point P generates a force and acts on a fresh charge, q. The electric field produced by a charge Q at r can be calculated in the following way: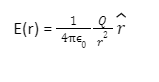 Where r is a unit vector from the origin to r, as a result, for each value of the position vector r, the above statement provides the electric field value.
The presence of an electric field due to a point charge is related to the action of a charge.
The force F that a charge Q exerts on another charge q is computed as:
Where r is a unit vector from the origin to r, as a result, for each value of the position vector r, the above statement provides the electric field value.
The presence of an electric field due to a point charge is related to the action of a charge.
The force F that a charge Q exerts on another charge q is computed as:
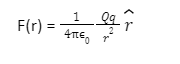 If the charge q is symbolised by the vector r, it feels a force F equal to the charge q multiplied by the electric field E at the location of q.
As a result, F(r) = q x E(r)
If the charge q is symbolised by the vector r, it feels a force F equal to the charge q multiplied by the electric field E at the location of q.
As a result, F(r) = q x E(r)
Electric field due to a system of charges
Consider a system of charges q1, q2,…, qn with r1, r2,…, rn location vectors with respect to some origin O. The electric field at a point in space due to a system of charges We have to use Coulomb’s law and the principle of superposition.The electric field E1 caused by q1 at r1 is expressed as,
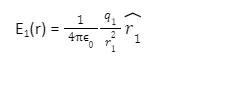 Here r1 is the distance between q1 and P, and r1 is the unit vector in the direction from q1 to P.
Here r1 is the distance between q1 and P, and r1 is the unit vector in the direction from q1 to P.In the same way, the electric field E2 cause by q2 at r2 can be written as,
Here r2 is the distance between q2 and P and r2 is the unit vector in the direction from q2 to P. Charges q3., q4…, qn cause similar expressions for fields E3, E4…, En . The electric field E due to the system of charges can be represented as follows using the superposition principle:
E(r) = E1 + E2 + E3 …………+ En . ( All in vector form )
The source charge positions determine E, which is a vector variable that varies from one location in space to another.
Electric Potential
The difference in potential energy per unit charge between two points in an electric field is known as the electric potential difference between the two points. EnergyCharge = electric potential difference (V)Electric potential due to multiple charges
The electric potential at a point due to a group of point charges is the algebraic sum of all the potentials due to all the individual charges. It’s written as,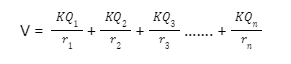
Conclusion
A source charge Q generates an electric field, while a test charge q assesses the effect of a source charge Q. The electric field due to a point charge Q at a location r is given by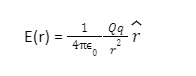 The amount of work energy necessary to shift a unit of electric charge from a reference point to a specific place in an electric field is known as electric potential energy.
The amount of work energy necessary to shift a unit of electric charge from a reference point to a specific place in an electric field is known as electric potential energy.