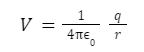
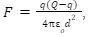
What is Equipotential Surface
An equipotential surface is the contact points in space having the same potential on the surface. Equipotential means that a charge will have the same potential energy at every point on the equipotential surface.
For a single charge q, the potential is given by,
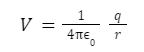
Where
q = point charge
r = distance between to connecting layers
εo= electric constant
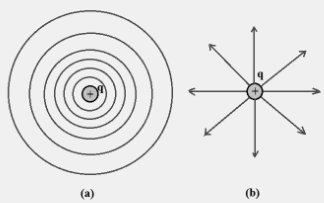
This indicates that V always exists when r does not change. Therefore, the same single-point charging points are circular-focused charging circuits.

Now, single power chargers q are radial lines that start or end in control, depending on whether q is positive or negative. Obviously, the electric field in all areas is common in the equipotential area that exceeds that point. This is generally true: in any charge configuration, the equipotential location through a point is common in the electric field at that time. Evidence of this statement is simple. If the field were unfamiliar in the equipotential area, it would have non-zero parts in the area. But this contradicts the equipotential equivalent definition: no distinction can be made between any of the two points above, and no function is required to move the test payout upwards. Therefore, the electric field should be normal in the equipotential area at all points. Equivalent locations provide another visual image in addition to the image of the electric field lines near the charging configuration.

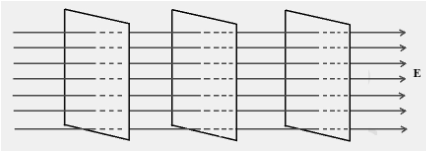
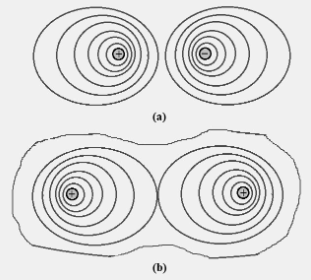
With the same electric field E, that is, near the x-axis, the equations are the normal plane on the x-axis, i.e., planes that align with the y-z plane. Equivalent figures of (a) dipole and (b) equilibrium are shown in the figure below.

Equipotential Lines
If points in the whole electrical field have the same electrical potential, then they are known as equipotential points. When these points are connected by a line or curve, it is known as an equipotential line.
Work Done in Equipotential Surface
The work done on the energy transfer between the two points at equipotential is zero. Therefore, W = 0
Properties of an Equipotential Surface
- The amount of electrical energy is the same throughout the surface
- The electric field is directed to the electric field standard
- The two equipotential areas do not meet
- The internal power of the empty charged charge conductor has not changed; this is considered equipotential volume
- For a single point charge, equal areas are in the circular position
- The space between the equipotential areas allows us to see the strong and weak field regions
Problems Based on the Concept of Equipotential Surface
Problem 1: A charge Q is to be divided into two objects. What should be the values of the charges on the objects so that the force between the objects can be maximum?
Solution:
Suppose one object receives a charge q and the other Q − q. The force between the objects is
where d is the separation between them. For F to be maximum, the quantity
y=q(Q-q)=Qq-q2
should be maximum. This is the case when
dy/dq = 0 or, Q − 2q = 0 or, q=Q/2.
Thus, the charge should be divided equally on the two objects.
Problem 2: In a circuit, 10 C of charge is passed through a battery in a given time. The plates of the battery are maintained at a potential difference of 12 V. How much work is done by the battery?
Solution:
By definition, the work done to transport a charge q through a potential difference V is qV. Thus, work done by the battery
=10 C * 12 V = 120 J.
Problem 3: An HCl molecule has a dipole moment of 3.4 × 10–30 Cm. Assuming that equal and opposite charges lie on the two atoms to form a dipole, what is the magnitude of this charge?
The separation between the two atoms of HCl is 1.0 × 10 –10 m.
Solution:
If the charges on the two atoms are q, − q,
q(1.0 × 10–30 m) = 3.4 × 10–30 Cm
q = 3.4 × 10–20 C.
Conclusion
- An equipotential surface is the collection of points in space that are all at the same potential.
- Equipotential lines are the two-dimensional representation of equipotential surfaces.
- Equipotential areas remain perpendicular to the electric field lines
- The part of the electric field corresponding to the equipotential equilibrium is zero, as the force does not change in this case. Thus, the electric field is perpendicular to the equipotential surface of each area