Our investigation of one-dimensional kinematics has been focused on the various ways in which the motion of objects can be represented mathematically and numerically. Verbal communication, diagramming communication, numerical communication, equational communication, and graphing communication are examples of such methods. When describing motion, velocity versus time graphs is used to help you understand what’s going on. In a velocity against time graph, the form and slope of the lines reflect the precise characteristics of an object’s motion.
Speed time graphs
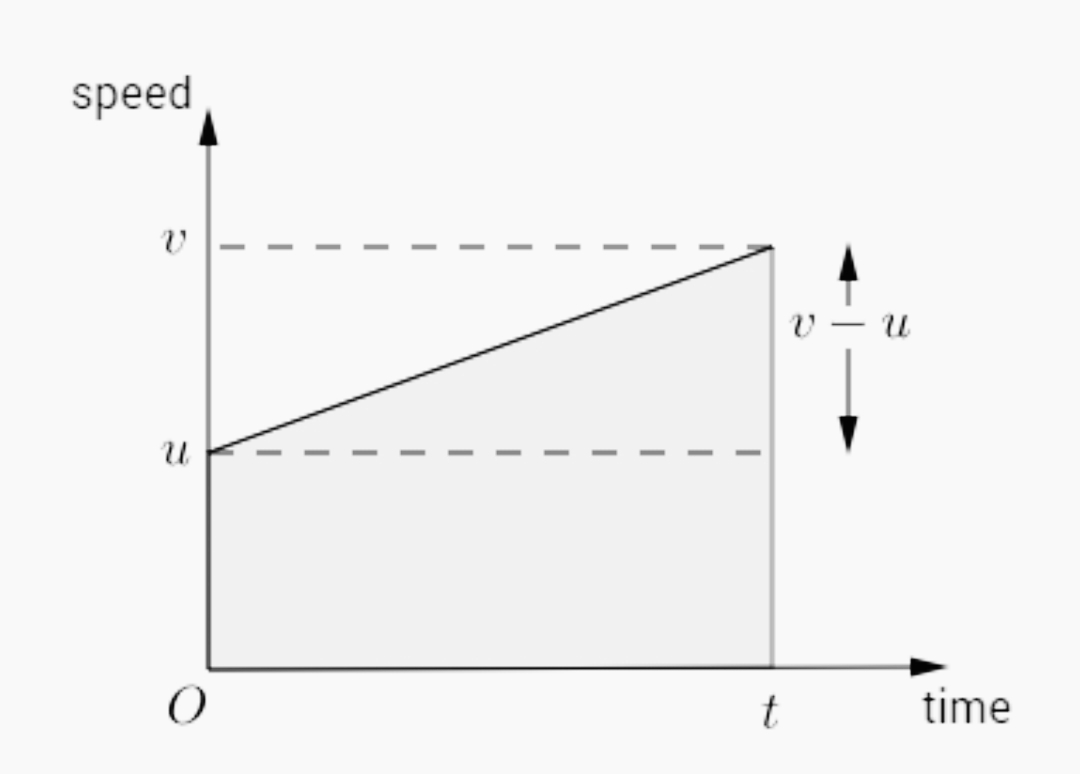
Speed time graphs are a very useful tool because they allow us to define the motion of an item over any given period of time, which is incredibly useful. Using a speed-time graph, you can determine the acceleration of an object, the average speed of the object at any given point in time, the total distance travelled, the total time it took the body to travel that distance, and whether or not the body was in motion at a given point in time, among other things. The speed of the object is displayed along the y axis of the graph, and the time it takes for the object to move along the x-axis of the graph is plotted on the x-axis. The distance travelled is shown by the area under the speed-time plot. When the values of speed with respect to time are plotted on a graph, and we obtain a sloping line, this indicates that the item is experiencing positive acceleration, and the slope of the line provides us with the value of acceleration. The higher the angle formed by the slope with regard to the x-axis, the greater the value of acceleration is expected to be. When the slope goes downhill from right to left, on the other hand, it indicates that the item has slowed down during that period of time. However, if there are no slopes across the graph, the item is said to have moved at a constant speed throughout.
here,
v = final velocity
u = initial velocity
Speed
In general, speed can be defined as the rate at which the distance travelled by an object changes over a certain period of time. Speed is a scalar quantity since it solely refers to the magnitude of the movement rather than the direction. The formula for calculating speed is s=d/t, where s denotes the speed, d denotes the distance travelled by the object, and t denotes the amount of time it took the object to travel that distance. M/s (metre per second) is the international standard unit of speed, although km/h (kilometre per hour) is the most often used measure of speed across the world, except in North America and Europe, where mph (miles per hour) is the preferred unit of speed (miles per hour).
Instantaneous Speed is the observed speed of an object in motion at a certain point in time or for a brief period of time. It is also referred to as absolute speed. At a specific instant, it is given by the equation v=ds/dt, where v denotes the instantaneous speed and ds/dt is the rate of change of distance/position.
Average Speed: In contrast to instantaneous speed, average speed provides us with the value of speed throughout the complete duration of the entire time frame in question. Consider the following scenario: a vehicle travels 500 kilometres in 10 hours. In that situation, the average speed is calculated using the formula v=s/t and is determined to be 50 kilometres per hour. However, it is highly doubtful that the car maintained a steady speed of 50 kilometres per hour throughout its 10-hour excursion.
Tangential Speed (also known as tangential velocity) is the speed at which an object moves in a circular route. V=r, v denotes the tangential speed, ω the rotational speed, and r denotes the distance between the two points. The rotating speed is less fast near the centre and increases in value as we move out from the centre of the planet.
Types of speed-time graph
There are 3 types of speed-time graphs for an object.
-
speed-time graph when speed remains constant
-
speed-time graph when speed changes at a uniform rate.
-
speed-time graph when a speed changes at a non-uniform rate.
What does the speed-time graph show?
When it comes to describing the movement of an object, speed-time graphs are extremely useful.
These measurements can be used to establish whether or not an object is moving at any given point in time. We can also use them to determine the speed at which an object is moving at any given point in time.
We may determine any acceleration, the change in speed, and the change in time, based on the data on the graph.
In addition, we can use graphs to compute the distance travelled. In a speed-time graph, the distance travelled is represented by the area under the graph.
Conclusion
Using a speed-time graph, you can determine the acceleration of an object. You can also determine the average speed of the object at any given point in time. In general, speed can be defined as the rate at which the distance travelled by an object changes over a certain period of time. Tangential Speed (also known as tangential velocity) is the speed at which an object moves in a circular route. At a specific instant, it is given by the equation v=ds/dt, where v denotes the instantaneous speed and ds/dt is the rate of change of distance/position.