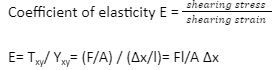
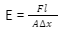
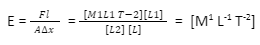
The coefficient of elasticity or modulus of elasticity is the measurement of the elastic property of a material. When a force is applied to a material, its extent of getting distorted varies from material to material. This constant gives an idea about the degree of distortion. Elasticity is represented using δ.
Dimensional Formula
The dimensional formula of any bodily amount is defined as the expression that represents how and which of the bottom portions are protected in that amount. It is denoted through enclosing the symbols for base portions with suitable strength in rectangular brackets [].
An example is the Dimension Formula of Mass which is given as [M].
Application of Dimensional Analysis
In real-life physics, dimensional analysis is a crucial part of the measurement. We use dimensional analysis for 3 main reasons:
- To ensure that a dimensional equation is consistent.
- Determining the relationship between physical quantities in physical phenomena
- To switch from one system to another’s units.
- Development of a fluid phenomena equation.
- The number of variables necessary in an equation is reduced.
Limitations of the dimensional equation
- The principle of homogeneity of dimensions cannot be used for trigonometric and exponential expressions. The derivation is more complex and complicated.
- The comparing terms or factors are less.
- The correctness of the physical expressions depends only on dimensional equality.
- It is majorly used in the case of dimensional constants. We are not able to find the value of the dimensionless constant.
Dimensional Formula of Coefficient of Elasticity
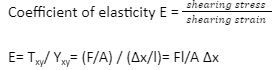
Here, Txy= F/A is the shear stress;
An object experiences force F;
An area where a force is exerted is A;
Shear strain is Yxy= Δx/l;
Transverse displacement is represented by Δx.
The initial length of material is l
It is a particular form of Hooke’s law of elasticity.
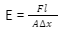
We know that dimension of force = [M¹L¹ T-²]
dimension of length = [L¹]
dimension of area = [L²]
dimension of Δx = [L]
Now put the values in equation
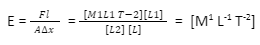
dimensional formula of Coefficient of Elasticity = [M¹ L-¹ T-²]
Coefficient of elasticity
- Coefficient of elasticity is the measurement of the elastic property of any material. It is expressed as the ratio of stress vs strain.
- In other words modulus of elasticity or coefficient of elasticity can also be defined as the amount of stress developed inside a material in resistance against the external distorting force due to unit strain is called coefficient of elasticity.
- Depending upon the different types of materials we usually define it in 3 ways-Young Modulus, Bulk Modulus, and Shear Modulus. In all these 3 kinds of moduli, the external force acts in the same way but the only difference is the type of distortion the object is showing due to the external force.
Unit of Coefficient of elasticity (COE):
The SI unit for COE is newton/m2 = Pascal
Elasticity and its Behaviour
- When stress application stops, the body regains its unique shape and size. Various materials show diverse elastic behaviour.
- The study of a material’s flexible behaviour is extremely important. Almost every design plan necessitates knowledge of a material’s flexible conductivity.
- For example, while building a bridge, the amount of traffic that it can bear should be properly measured in advance.
- Similarly, when building a crane to lift loads, it is important to remember that the rope’s extension does not exceed its elastic limit.
- The elastic behaviour of the material utilised must be considered first to solve the problem of bending under stress.
Elastic Behaviour of solids
The atoms or molecules inside a solid body are shifted from their specified points or fixed points (equilibrium positions) when it is deformed, resulting in a shift in interatomic and molecular distances. The interatomic force strives to return the body to its initial position when this force is withdrawn. As a result, the body returns to its former shape.
Thus, the material can get distorted depending on the force applied to it. The force that causes the change in the relocation of these particles is known as the twisting force.
As we know that any force has its inverse and equivalent force, which acts in the opposite direction. After the disfiguring force has been expelled, this force encourages the body to regain its original condition.
Conclusion
In this article, we learned the basics of the coefficient of elasticity and its dimensional analysis. Elastic coefficients are very important. While we choose material for different purposes. For example, if we require a product that has to be tensile then we have to choose a material with a higher value of elasticity.