Introduction
A quadrilateral is a four-sided polygon in the field of geometry. The different quadrilaterals are the square, rectangle, rhombus, parallelogram, kite, and trapezium, all of which have some traits in common with one another. It is well known that the rhombus and the parallelogram are both termed quadrilaterals due to the fact that they have four sides each. Due to the fact that the opposing faces of a parallelogram are parallel, the opposing angles of the form are equal as well. However, in a rhombus, all four sides are of equal length, whereas in a parallelogram, only the two sides that are opposite each other are of equal length. Both the two-dimensional shapes of rhombus and parallelogram are not the same when several of their attributes are taken into consideration. A rhombus is a shape that can be thought of as a subset of the shape parallelogram.
Rhombus
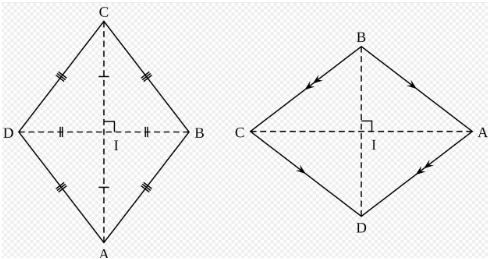
When it comes to planar Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral with four sides that are all of the same length (or lengths). Another term for this shape is the equilateral quadrilateral because equilateral refers to the fact that all of its sides are of equal length. Although the rhombus is sometimes referred to as a diamond, after the diamonds suit in playing cards, because it resembles the projection of an octahedral diamond, it is also referred to as a lozenge, though the former term sometimes refers specifically to a rhombus with a 60° angle and the latter term sometimes refers specifically to a rhombus with a 45° angle. There are no self-intersecting rhombuses; instead, they are a subset of the parallelogram and the kite. A square is formed by a rhombus with right angles.

Characteristics of rhombus
A rhombus is formed by a simple (non-self-intersecting) quadrilateral if and only if it is any one of the following shapes:
- the diagonal of a parallelogram bisects the inner angle of a parallelogram.
- a parallelogram in which at least two consecutive sides are of identical length.
- a parallelogram whose diagonals are perpendicular to each other (an orthodiagonal parallelogram).
- a quadrilateral with four sides that are all of the same lengths.
- a quadrilateral in which the diagonals are perpendicular to each other and bisect the middle diagonally.
- a quadrilateral in which each diagonal bisects two interior angles that are diametrically opposed.
- In the plane of the quadrilateral ABCD, there is a point P such that the four triangles ABP, BCP, CDP, and DAP are all congruent.
- a quadrilateral ABCD in which the incircles in the triangles ABC, BCD, CDA, and DAB have a common point is formed by joining the triangles ABC, BCD, CDA, and DAB.
Properties of a Rhombus
Because it possesses all of the characteristics of a parallelogram, a rhombus is regarded to be one of the exceptional parallelograms. The two diagonals of a rhombus serve as the two lines of symmetry of the shape. The axis of symmetry can be thought of as a line that divides an object into two equal halves when viewed from the side. It provides a mirror-like reflection of both sides of the object when used in conjunction with another object. A rhombus is said to have reflection symmetry across both of its diagonals if it has reflection symmetry over both of its diagonals. Generally speaking, a parallelogram has the following characteristics:
- Angles that are diametrically opposed are congruent or equal.
- The sides that are opposite each other are equal and parallel.
- Diagonals cut each other in half.
- The total of two adjacent angles is 180°.
In common with all geometric shapes, the rhombus possesses characteristics that are unique to it. The qualities of a rhombus are described in the following table.
Parallelogram
A parallelogram is a special type of quadrilateral that is produced by two parallel lines intersecting in the same direction. Although the angle between the adjacent sides of a parallelogram might vary, the opposite sides of a parallelogram must be parallel in order for it to be considered a parallelogram. If the opposite sides of a quadrilateral are parallel and congruent, the quadrilateral will be a parallelogram. In order to describe a quadrilateral in which both pairs of opposite sides are parallel and equal, a parallelogram is defined as follows: “Bounded by parallel lines” is how the term “parallelogram” was obtained from the Greek word “parallelogrammon,” which means “bounded by parallel lines.” An example of this is the parallelogram, which is a quadrilateral that is bordered by parallel lines.
Properties of a Parallelogram

The following characteristics of a parallelogram can be used to identify and distinguish it from other shapes:
- Parallelograms have opposite sides that are parallel to one another. In this case, PQ ‖RT and PR‖ QT.
- The sides of a parallelogram that are opposite each other are equal. In this case, PQ = RT and PR = QT.
- The angles on either side of a parallelogram are the same. In this case, P = T and Q = R.
- The diagonals of a parallelogram are perpendicular to one another. In this case, RE = EQ and PE = ET.
- Interior angles on the same side of the room are complementary to one another. In this case, ∠PRT + ∠RTQ = 180∘, ∠RTQ + ∠TQP = 180∘, ∠TQP + ∠QPR = 180∘, ∠QPR + ∠PRT = 180∘
- The diagonals divide the parallelogram into two congruent triangles, which are represented by the arrows. When RPQ is congruent to QTR, and when RPT is congruent to QTP, we have a congruent pair.
Conclusion
The angles on either side of a parallelogram are the same. The sides of a parallelogram that are opposite each other are equal. The diagonals of a parallelogram are perpendicular to one another.
Both the parallelogram and the rhombus are quadrilaterals, with facing sides that are parallel, opposite angles that are equal, and a total of the interior angles that is 360 ° for both shapes. A rhombus is a specific type of parallelogram in and of itself. As a result, it is feasible to say that every rhombus is a parallelogram, but the converse is not true.