
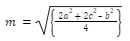
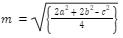
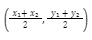
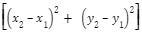
A line segment connecting a vertex of a triangle to the middle of the opposing side, bisecting that side, is known as the median of a triangle in geometry. There are three medians in every triangle, one from each vertex. The triangle’s centroid is where their medians cross. In this article, we’ll look at the attributes, definition, and formula for the median of a triangle.
Definition
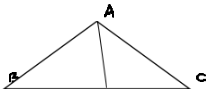
The median of a triangle is a line segment that connects a vertex to the midpoint of the opposing side. In the diagram below, AD represents the median, while BC is divided into two equal pieces, resulting in BD = DC.

Properties of Median of a Triangle
The following properties can be used to readily identify the median of a triangle:
- The median of a triangle is a line segment that connects the triangle’s vertex to the opposite side’s midpoint.
- It divides the opposite side into two equal portions by bisecting it.
- The middle of a triangle divides it into two triangles of equal area.
- A triangle’s three medians meet at a single point, regardless of its shape or size.
- Each vertex of a triangle has three medians. The triangle’s centroid is formed by the convergence of three medians.
- A triangle’s middle divides the triangle into two smaller triangles with equal areas. In fact, the three medians divide the triangle into six equal-sized triangles.
Altitude and Medians of the Triangle
The altitude and the median of a triangle are not the same things. The line segment that connects the vertex to the midpoint of the opposing side of the triangle is called the median. Regardless of the triangle’s nature, it has three medians (one from each vertex) that meet at a single point. The three medians meet at the triangle’s centroid, which is positioned inside the triangle. A median always cuts the side on which it is constructed in half.
A line segment connecting the vertex to the opposite side of the triangle at a right angle (90°) is defined as the triangle’s altitude. Depending on the form of the triangle, an altitude can be found within or outside. All triangles have three elevations (one from each vertex), which meet at the Orthocenter, a single point in the triangle. Inside or outside the triangle, the orthocenter can be found. The opposing side on which an altitude is produced does not always have to be bisected.
Formula for the Median of the Triangle
A basic formula that applies to all three medians can be used to find the median of a triangle. Let’s look at the formula for calculating the length of each median.
The first median of a triangle is calculated using the formula below, where the triangle’s median is m, the sides are a, b, and c, and the median is generated on side ‘a’.
![]()
The formula for calculating the second median of a triangle is as follows: where the triangle’s median is m, the sides are a, b, and c, and the median is formed on side ‘b’.
![]()
The formula for the third median of a triangle is as follows; the triangle’s median is m, the triangle’s sides are a, b, and c, and the median is formed on side ‘c’.
![]()
Finding the median of a triangle with given coordinates of vertices:-
When the coordinates of a triangle’s three vertices are known, we can use the steps below to calculate the length of the triangle’s median.
Step 1: Find the coordinates of the midpoint of the line segment on which the median is formed using the coordinates of the triangle’s vertices. The midpoint formula can be used to do this.
![]() the formula for midpoint, where (x1, y1) and (x1, y1) are the line segment coordinates.
the formula for midpoint, where (x1, y1) and (x1, y1) are the line segment coordinates.
Step 2: After obtaining the midpoint coordinates, use the distance formula to calculate the length of the median, where one endpoint is the vertex from which the median begins and the other is the midpoint of the line segment on which the median is constructed.
Step 3: Use the distance formula D = ![]() to find the median’s length, where (x1, y1) and (x1, y1) are the median’s coordinates.
to find the median’s length, where (x1, y1) and (x1, y1) are the median’s coordinates.
Tips on median of the triangle:-
- The triangle is divided into two smaller triangles with the same area by each median.
- The triangle’s centre of gravity is the centroid (the point where they meet).
- A triangle’s perimeter is larger than the sum of its three medians.
- Because the corresponding sections of congruent triangles are congruent, the medians of congruent triangles are equal if the two triangles are congruent.
Conclusion
A triangle’s median is a line segment that connects a vertex to the opposing side’s midpoint, effectively bisecting that side. Each vertex has three medians, which intersect at the triangle’s centroid. Any angle at a vertex whose two adjacent sides are identical in length is bisected by a median in isosceles and equilateral triangles.