A significant area of mathematics called geometry deals with various figures and shapes. The mid-point theorem directs attention to the midpoints of triangles, which are significant geometric figures.
The line segment connecting the midpoints of two triangle sides is parallel to and makes up half of the third side, according to this theorem.
Mid-point Theorem:
The mid-point theorem in geometry aids in determining the angles of triangles that are missing values. It provides a connection between a triangle’s sides and the line segment formed by the midpoints of any two of the triangle’s sides. According to the midpoint theorem, the line segment drawn from the intersection of any two triangle sides is parallel to the third side and equal to half of its length.
We will examine the idea of the midway theorem and its opposite in this post. A few solved cases will be used to teach us how to apply the theorem so that we may better understand the idea.
Midpoint Theorem: What is it?
According to the midpoint theorem, the line segment connecting any two triangle sides’ midpoints is parallel to the third side and equal to half of its length. The midpoint theorem can be used to cut a stick in half without a measuring device in a number of different situations in everyday life.
Defined midpoint theorem
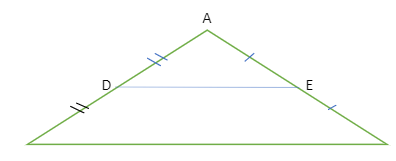
According to the midpoint theorem, the line segment connecting any two triangle sides’ midpoints is parallel to and equal to half of the third side. Think of the ABC triangle as an example. The midpoints of AB and AC, respectively, should be D and E. Let’s say you connect D and E. According to the midpoint theorem, DE will be equal to exactly half of BC and parallel to BC. To comprehend the triangle midpoint theorem, look at the illustration provided below.

DE || BC, DE = ½ of BC
Proof of the Midpoint Theorem
Let’s now express and substantiate the midway theorem. The length of the third side is equal to the distance along a straight line that connects any two triangle sides at their midpoints. Think about the ABC triangle, as seen in the illustration below. Assume that E and D represent the middles of sides AC and AB, respectively. The side DE is half of the side BC, or DE || BC, so the line DE is then said to be parallel to the side BC.
DE = 1/2 × BC
The midpoint theorem is stated in this manner. Let’s now examine its evidence. C.
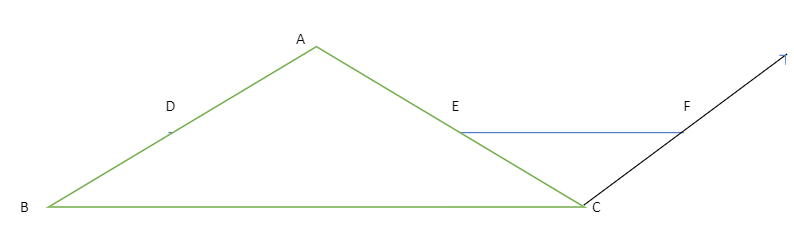
Given: The midpoints of sides AB & AC of ∆ABC are D and E, respectively.
Drawing a line parallel to BA through ∆ABC and extending DE so that it intersects this line at F is the construction required.

Proof: AED and CEF are contrasted:
AE = EC (E is the midpoint of AC)
Angle DAE = angle FCE (alternate interior angles)
Angle FEC = angle DEA (vertically opposite angles)
The two triangles satisfy the ASA requirement. As a result, DE = EF and AD = CF. However, AD is also equivalent to BD, therefore by our design, BD = CF and BD || CF. By extension, BCFD must be a parallelogram. Since a result, DF = BC DE = 1/2 BC and DF = BC DE + EF = BC 2DE = BC (as DE = EF, as proved before).
This concludes our case. Will the midway theorem’s opposite hold true? Yes, it will, and the evidence for the opposite is then shown.
Converse of the Midpoint Theorem:
According to the reverse of the midpoint theorem, a line drawn through the middle of one triangle’s side and parallel to another side will cut through the third side. Let D represent the middle point of the triangle ABC. As shown below, a line via D that runs parallel to BC intersects AC at E. Consider the scenario where E is not AC’s midpoint. Let F represent AC’s midway. As indicated below, connect D to F.
The midpoint theorem states that DF || BC. But there is also DE || BC. This is impossible because only one parallel can be traced to a given line through a given point, in this case, D. (in this case, BC). E must therefore be AC’s midway.
Defining the Midpoint Theorem
There is a midpoint theorem formula in mathematics that is used in coordinate geometry. Theorem of a line segment midpoint is another name for it. It says that if a line segment’s endpoints are supplied as (x1, y1) and (x2, y2), we can use the following formula to obtain the coordinates of the line segment’s midpoint:
Let the midpoint of the line segment’s coordinates be (xm, ym). As a result, (xm, ym) = ((x1 + x2)/2, (y1 + y2)/2).
The midpoint theorem equation is what this is.
Sides Connecting a Triangle’s Midpoints
A fascinating result of the midpoint theorem is that, as illustrated in the following diagram, if we unite the midpoints of any triangle’s three sides, we will obtain four (smaller) congruent triangles.
We have ADE, FED, BDF, and EFC.
Proof: Think about the DEFB quadrilateral. The midway theory gives us:
BC = BF DE = 1/2
DE || BF
Since DEFB is a parallelogram as a result, FED BDF. Additionally, we can demonstrate that AEFD and DECF are parallelograms, and as a result, all four of the resulting triangles are congruent with one another (make sure that when you write the congruence relation between these triangles, you get the order of the vertices correct).
Conclusion:
According to the midpoint theorem, the line segment connecting any two triangle sides’ midpoints is parallel to this side and equal to half of its length. According to the reverse of the midpoint theorem, a line drawn through the middle of one triangle’s side and parallel to another side will cut through the third side.