Points that sit on the same straight line are known as collinear points. They don’t have to be coplanar, but they do have to be on the same straight line. Collinear comes from the Latin terms ‘col’ and ‘linear,’ where ‘col’ means together and ‘linear’ means in the same line. A point on a plane determines its location in geometry. On a plane, we can mark any number of points. Assume you mark three points on paper and are required to label them with a single capital letter such as A, B, C or P, Q, R because the points must be represented using capital letters.
Collinear Points
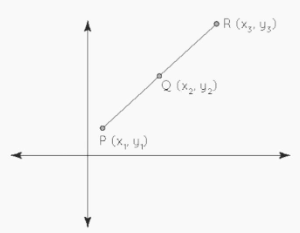
A group of three or more points on the same straight line is known as a collinear point. On separate planes, collinear points may exist, but not on different lines. Collinearity is the property of points being collinear. As a result, any three or more points are only collinear if they are in the same straight line. There is only one line that can pass through three separate collinear points. Consider the diagram below, in which the collinear points are P, Q, and R.
Collinear Points Formula
To determine whether three points are collinear, use the collinear points formula. There are several methods for determining whether or not three points are collinear. The Slope Formula, the Area of Triangle Formula, and the Distance Formula are the three most prevalent formulas for determining whether or not points are collinear.
Slope Formula
To find the slope of lines generated by the three locations in question, we use the slope formula. The three points are collinear if their slopes are equivalent.
If we have three points X, Y, and Z, for example, the points will only be collinear if the slope of line XY = slope of line YZ = slope of line XZ. The slope formula is used to determine the slope of a line connecting two locations.
The line connecting points P(x1, y1) and Q(x2, y2) has the following slope: (y2 – y1) / (x1 – x2).
Area of Triangle Formula
We leverage the fact that a triangle cannot be constructed by three collinear points in this method. This indicates that no triangle can be formed if any three points are collinear. As a result, we check the triangle’s points by plugging them into the calculation for triangle area. Those points will be deemed collinear if the area is equal to zero. In other words, because the triangle produced by three collinear points is essentially a line connecting the three points, it has no area.
The area of the triangle having the given points (vertices) A(x1, y1), B(x2, y2), and C(x3, y3) is:
½ | x1(y2 – y3) + X2 ( y3 – y1) + X3 ( y1 – y2 ) |
If the area is equal to zero, the points are considered collinear.
Distance Formula
We find the distance between the first and second points, then the distance between the second and third points, using the distance formula. Then we determine whether the sum of these two distances equals the distance between the first and third points. Only if the three points are collinear will this be achievable. The distance formula is used to compute the distance between two places whose coordinates are known.
A(x1, y1) and B(x2, y2) are separated by the following distance:
AB = √ (x2 – x1 )² + (y2 – y1 )²
So, if we have three collinear points in the order A, B, and C, then AB + BC = CA.
- Only if three points are in the same straight line will they be collinear.
- Collinearity is the property of points being concentric.
- On different planes, collinear points might exist.
Conclusion
Lines can be parallel, perpendicular, intersected, and so on. Line slopes are related to one another in all of these cases. The slopes of two parallel lines, as we know, are equal. If two lines with the same slope intersect at the same point, the lines will coincide. To put it another way, if A, B, and C are three points in the XY-plane, they will lie on a line, i.e., three points are collinear if and only if the slope of AB equals the slope of BC.