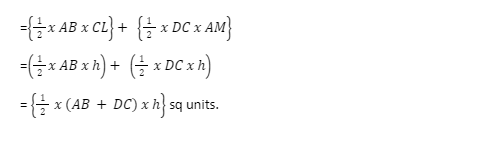
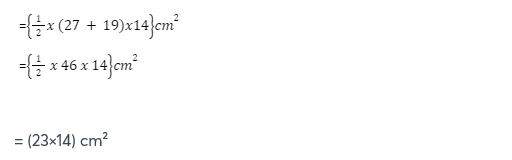

Mensuration is a discipline of mathematics that studies geometric shapes, their area, volume, and other associated properties. A trapezium is a kind of quadrilateral in which two of its sides are parallel and two are non-parallel. The two parallel sides of a trapezium are known as base. And (h) is considered to be the height/ altitude of the trapezium or the distance between two parallel sides. If the non-parallel side of a trapezium is equal then it will be an isosceles trapezium.
Formula of trapezium
Area of trapezium = 1/2 x (sum of parallel sides) x (distance between them)
Area of trapezium formula proof
Let ABCD be a trapezium of height h and AB||DC
Join AC and draw perpendicular CL on AB and produce DC and draw perpendicular AM on DC.
Let CL and AM = h
Area of trapezium = area of ∆ABC x area of ∆ACD
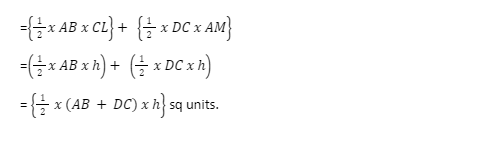 ∴ Area of trapezium = 1/2 x sum of parallel sidesx( distance between them)
∴ Area of trapezium = 1/2 x sum of parallel sidesx( distance between them)
Properties of trapezium
- Trapezium is a closed figure in which sum of interior angles is equals to 360°
- It has a pair of the parallel side that are opposite to each other and both of them are known as base.
- The other two sides of a trapezium should be non-parallel and if these non-parallel sides of a trapezium are equal to each other then, the trapezium is said to be an isosceles trapezium.
- In trapezium sum of adjacent angles is equals to 180°
- At their intersection, the trapezoid’s diagonals cut each other in half.
Some questions based on trapezium
Q1. Two parallel sides of a trapezium are of lengths 27 cm and 19 cm respectively. And the distance between them is 14cm. Find the area of trapezium
Solution –area of trapezium = ½ x (sum of parallel side) x (distance between them)
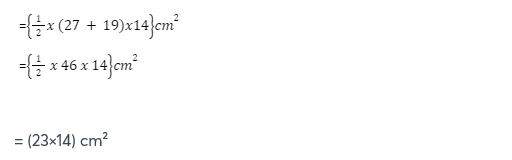
= 322 cm²
Q2. The area of a trapezium is 352 cm² and the distance between its parallel sides is 16cm. If one of the parallel sides is of length 25cm, find the length of the other.
Solution – Given, the area of trapezium is 352 cm2.
Distance between its parallel side = 16cm
One side is 25 cm
Let the other side be x
Then by using formula –
 325 = (200 + 8x) cm².
325 = (200 + 8x) cm².
8x = (352 – 200)
8x = 152
x = (152/8)
x = 19.
Some practice questions based on the trapezium
Q1. Find the area of a trapezium whose parallel sides are 24 cm and 20 cm and the distance between them is 15 cm.
Q2. Find the area of a trapezium whose parallel sides are 38.7 cm and 22.3 cm, and the distance between them is 16 cm.
Q3. The area of a trapezium is 1080 cm². If the lengths of its parallel sides are 55 cm and 34.4 cm, find the distance between them.
Q4. The area of a trapezium is 1586 cm² and the distance between its parallel sides is 26 cm. If one of the parallel sides is 84 cm, find the other.
Q5. The area of a trapezium is 405cm². Its parallel sides are in the ratio
4 : 5 and the perpendicular distance between them is 18 cm. Find the length of each of the parallel sides.
Conclusion
Mensuration is a discipline of mathematics that studies geometric shapes, their area, volume, and other associated properties. A trapezium is a quadrilateral in which two of its sides are parallel and two are non-parallel. (h) is considered to be the height/ altitude of the trapezium or the distance between two parallel sides. It has a pair of parallel side that are opposite to each other and both of them are known as based. If the non-parallel side of a trapezium is equal then it will be an isosceles trapezium.
Important Pages
JEE Full Form | LCD Full Form | ABS Full Form | EPC Full Form |
IIT Full Form | CFL Full Form | SCR Full Form | TFT Full Form |
IELTS Full Form | SONAR Full Form | LED Full Form | mAh Full Form |