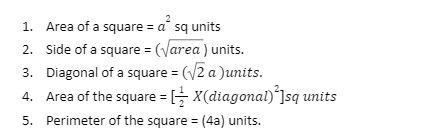

Introduction
A square’s area is defined as the number of square units required to fill it. In other words, when calculating the area of a square, we take the length of its side into account. Due to the fact that all of a square’s sides are equal, its area is equal to the product of its two sides. The area of a square is commonly measured in square meters, square feet, square inches, and square centimeters. The area of a thing is the space that it occupies. It is the region that any shape occupies. Typically, the area of a figure can be calculated on a two-dimensional plane by considering only the shape’s surface. For instance, in the case of a square, we evaluate simply its side length.
Polygon
polygon, It is defined as “any closed curve consisting of a group of line segments (sides) joined together so that no two segments cross each other in geometry.” Pentagons (which have five sides) and triangles (which have three sides) are the easiest polygons to understand (five sides). If none of the sides overlap the polygon when the sides are extended, the polygon is convex; otherwise, the polygon is concave. Equilateral polygons are polygons with all of their sides equal. Equiangular shapes are those in which all interior angles are equal. Regular polygons are any polygons that are both equilateral and equiangular in shape (e.g., equilateral triangle, square).
What is a square?
A square is a quadrilateral having four sides that are all the same length. There are numerous objects in our environment that have the shape of a square. Each square form may be distinguished by its equal sides as well as its internal angles which are all 90 degrees. A square is a closed two-dimensional form (2D shape) with four sides that is closed in two dimensions. An equal and parallel relationship exists between each of a square’s four sides.
Formula of area of square
As a result of multiplying each side length by itself, you can find out how big a square it is by looking at the formula below. As a result, Area A is equal to the square root of the length of each side. In the case of a square with each side measuring 6 feet in length, the area is 6 times 6, or 36 square feet.
Formulas related to square-
Let us consider a square each of whose sides = a.
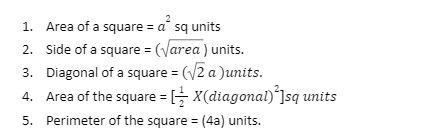

Some questions for practice
Q1. A square lawn is surrounded by a path 2.5m wide. If the area of the path is 165m2 , find the area of the lawn.
Q2. Each Side of a square flower bed is 2m 80cm long. It is extended by digging a strip 30cm wide all around it. Find the area of the endless flower bed and also the increase in the area of the flower bed.
Conclusion
When calculating the area of a square, we take the length of its side into account. A square is a quadrilateral having four sides that are all the same length. Area A is equal to the square root of each side’s length. Equiangular shapes are those in which all interior angles are equal. Pentagons and triangles are the easiest polygons to understand (five sides). Let us consider a square each of whose sides = a.