Mean Value Theorems
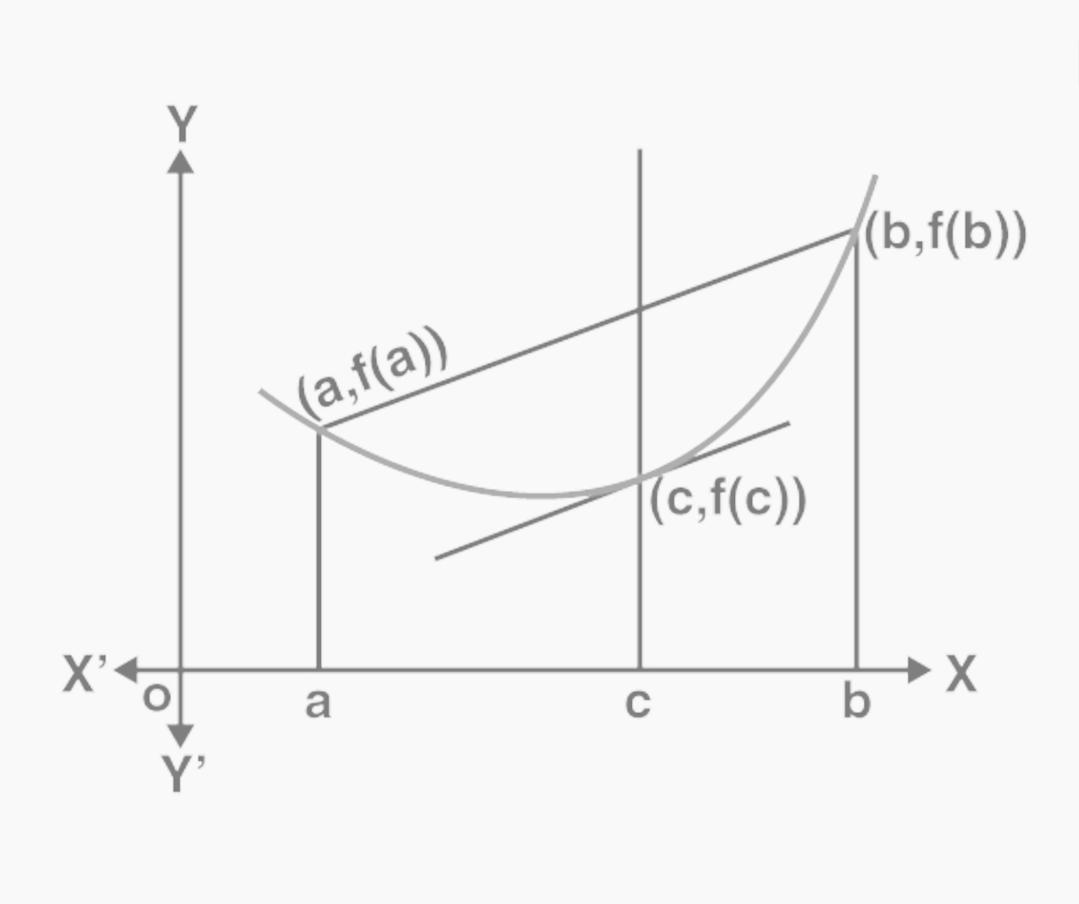
Specifically, for every curve f(x) passing through two specified points (a, f(a)) and (b, f(b)), the mean value theorem asserts that there is at least one point on the curve (c, f(c)) at which the tangent travelling through those two points is parallel to the secant travelling through those two locations. The mean value theorem is defined here in calculus for a function f(x): [a, b] →R, which is continuous and differentiable across an interval and has the properties of being continuous and differentiable.
•It is possible to consider the function f(x) as being continuous across the interval [a, b]
•The function f(x) is differentiable over the interval x = 0 to 1. (a, b)
•There is a point c in the coordinates (a, b) at which f'(c) = [f(b) – f(a)] / (b – a)
In this section, we have demonstrated that the tangent at c is parallel to the secant travelling through the points (a, f(a)), and (b, f(b). It is possible to prove a statement across a closed interval using this mean value theorem.
Rolle’s Theorem is a special case of the mean value theorem that is true if and only if specific conditions are met. At the same time, Lagrange’s mean value theorem is the mean value theorem itself, or the first mean value theorem, as the term is used in the literature. In general, mean can be thought of as the average of the values that have been provided. It is a different method in the case of integrals, however, when determining the mean value of two separate functions. Let us study Rolle’s theorem, the mean value of such functions, and the geometrical interpretation of these functions.
Lagrange’s Mean Value Theorem
It is possible to define a function f on the closed interval [a,b] that meets all of the following requirements:
i) The function f is continuous on the closed interval [a, b]
ii)In addition, the function f on the open interval (a,b) is differentiable
Then there is a value x = c that is defined in such a way that
f'(c) = [f(b) – f(a)]/(b-a)
This theorem is also referred to as the first mean value theorem or Lagrange’s mean value theorem, depending on who is talking about it.
Interpretation of Lagrange’s Mean Value Theorem from a Geometrical Perspective

If the curve y = f(x) is continuous between the points x = a and x = b and differentiable within the closed interval [a,b], then according to Lagrange’s mean value theorem, for any function that is continuous on [a, b] and differentiable on (a, b), there exists some c in the interval (a, b) such that the secant joining the endpoints of the interval [a, b] is parallel to the tangent at c.
f’c = f(b)-f(a)/(b-a)
The Rolle’s Theorem
The Rolle’s Theorem is a proof that
Rolle’s Theorem, which is a specific case of Lagrange’s mean value theorem, states that the following:
If a function f is defined in the closed interval [a, b] in such a way that it satisfies the following conditions, then the function f is said to satisfy the conditions.
i) The function f is continuous on the closed interval [a, b] .
ii)In addition, the function f differencing on the open interval is differentiable (a, b)
After all of this, let’s assume that there is at least one value of x that is between the two values of a and b, i.e. (a<c<b), and that this value is c; this value is assumed to be zero.
To put it another way, if a function is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), then there exists a point x = c in the open interval (a, b) where f'(c) = 0.
Rolle’s Theorem is given a geometric explanation

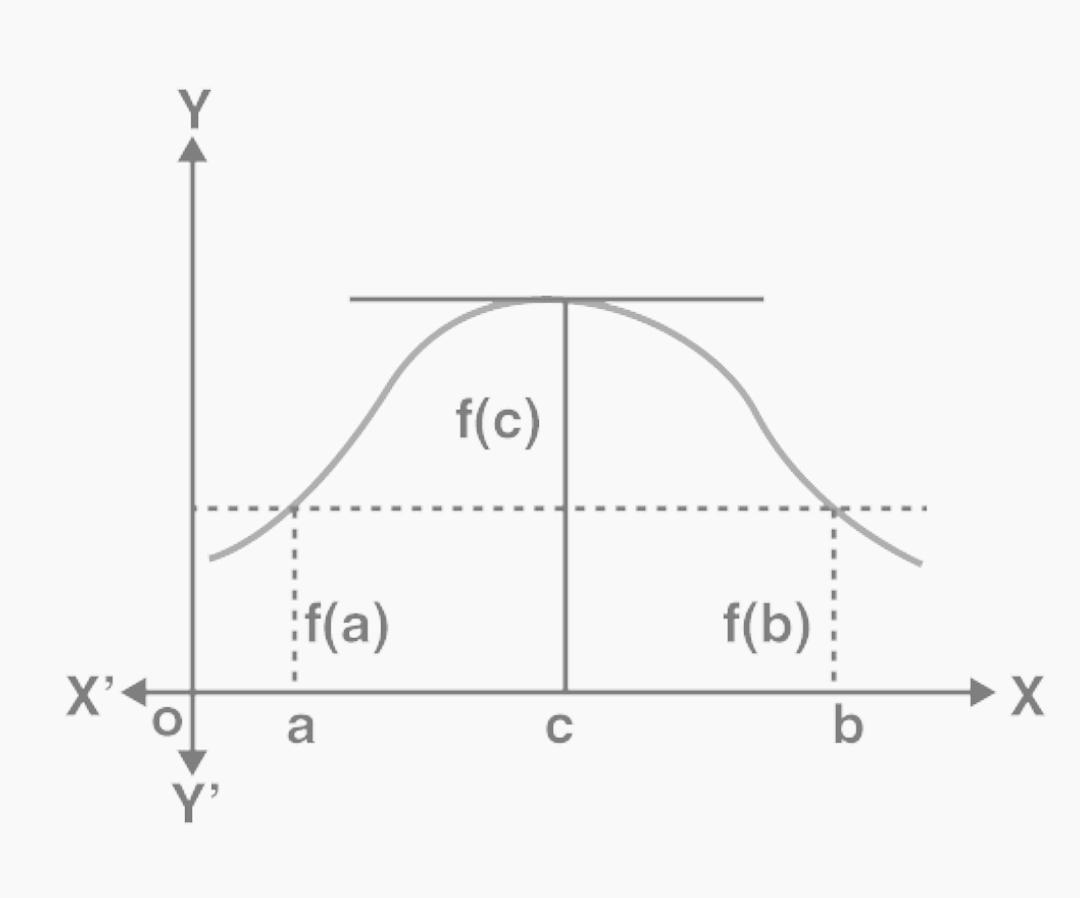
y = f(x) is continuous between x = a and x = b in the above graph, and at every point inside the interval, it is possible to draw a tangent to the curve, and ordinates that correspond to the abscissa and are equal, then there exists at least one tangent to the curve that is parallel to the x-axis.
When we look at this theorem from an algebraic perspective, it tells us that, given a polynomial function f (x) as its representation in x and two roots of the equation f(x)=0 as the values a and b, there exists at least one root of the equation f'(x) = 0 that lies between these values.
However, the converse of Rolle’s theorem is not true. Furthermore, there is a possibility that there are more than one value of x for which the theorem holds true; however, there is an extremely high probability of the existence of only one such value.
The Theorem of Rolle is as follows:
Rolle’s theorem can be expressed mathematically as follows:
Suppose f: [a, b] →R is a continuous function on [a, b] and differentiable on (a, b), such that f(a) = f(b), where the real numbers a and b are used as examples. In that case, there exists at least one c in (a, b) such that f′(c) = 0
Conclusion
The mean value theorem is defined here in calculus for a function f(x): [a, b] →R, which is continuous and differentiable across an interval and has the properties of being continuous and differentiable.Rolle’s Theorem is a special case of the mean value theorem that is true if and only if specific conditions are met. At the same time, Lagrange’s mean value theorem is the mean value theorem itself, or the first mean value theorem, as the term is used in the literature. In general, mean can be thought of as the average of the values that have been provided.