In both differential and integral calculus, the mean value theorem is one of the most helpful techniques. It has significant implications in differential calculus and aids in understanding the same behavior of several functions.
The mean value theorem’s hypothesis and conclusion are similar to those of the Intermediate value theorem. Lagrange’s Mean Value Theorem is another name for the mean value theorem. MVT is the abbreviation for this theorem.
Definition
The mean value theorem asserts, approximately, that for any planar arc between two endpoints, the tangent to the arc is parallel to the secant through its endpoints at least one point. It is one of the most significant findings in real-world interval .This theorem is used to prove statements about a function on an interval, starting with local hypotheses regarding derivatives at interval points. 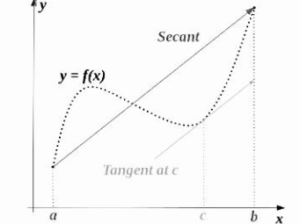
There is a value of c in the interval (a,b) such that the secant connecting the interval’s endpoints [a,b] is parallel to the tangent. At c for any function that runs indefinitely [a,b] and distinguishable on (a,b).
If f is a continuous function on the closed interval [a,b] and differentiable on the open interval (a,b), the theorem asserts that there exists a point c in (a,b) where the tangent at c is parallel to the secant line through the endpoints (a, f(a)) and (b, f(b)), that is, there exists a point c in (a,b) where the tangent at
f’(c) = [f(b) – f(a)] / (b – a)
Mean Value Theorem Statement
Assume f(x) is a function that meets the following criteria:
In [a,b], f(x) is Continuous.
If f(x) is Differentiable in (a,b), then a number c, s.t. a <c <b, exists.
Proof of Mean Value Theorem
The Mean Value Theorem can be demonstrated using the function h(x) = f(x) – g(x), where g(x) denotes the secant line AB. Rolle’s theorem can be applied to the continuous function h(x) to show that there is a point c in (a, b) where h’(c) = 0. The conclusion of the mean value theorem will be reached using this equation.
Consider a line that runs between (a, f(a)) and (b, f(b)). The line equation is
y – f(a) = {f(b) – f(a)}/(b-a) . (x – a)
Or y = f(a)+ {f(b) – f(a)}/(b-a) . (x – a)
Let h be a function that defines the difference between any f and the line above.
h(x) = f(x) – f(a) – {f(b)-f(a)}/(b-a) . (x – a)
We have used “Rolle’s theorem” to arrive at our conclusion.
h’(x) = f’(x) – {f(b)-f(a)}/(b-a)
Or f(b) – f(a) = f’(x) (b – a).
Hence Proved.
Mean Value Theorem for Integrals
The direct consequence of the first fundamental theorem of calculus and the mean value theorem is the mean value theorem for integrals. This theorem argues that if “f” is continuous over a closed limited interval, such as [a, b], then at least one number in c exists in (a, b).
f(c) = 1/b-a b∫a f(t)dt
Using the Mean Value Theorem for Integrals
The Mean Value Theorem for Integrals ensures that a rectangle with the same area and breadth exists for any definite integral. In addition, when this rectangle is superimposed on the definite integral, the top of the rectangle intersects the function. By the way, the mean-value rectangle for that definite integral is this rectangle. Its existence allows you to calculate the definite integral’s average value.
The intersection of the top of the mean-value rectangle with the function is mainly intuitive. After all, the height of this rectangle shows the function’s average value for a certain time span. On that interval, this value must be between the function’s maximum and minimum values.
Implications
Theorem 1: Assume f is a continuous, real-valued function defined on the real line’s arbitrary interval I. If the derivative of f exists and is zero at every interior point of the interval I, then f is constant in the interior.
Proof: Assume that the derivative of f exists and is 0 at every interior point of the interval I. Allow (a, b) to be any open interval in I. According to the mean value theorem, there is a point c in (a,b) where
0 = f’(c) = [f(b) – f(a)] / (b – a)
This means that f(a) = f(b) (b). As a result, f is constant on the interior of I and hence by continuity is constant on I. (For a multivariable version of this result, see below.)
Remarks
•At the endpoints of the interval I, just f continuity, not differentiability, is required. If I is an open interval, there is no need to express a continuity hypothesis because the existence of a derivative at a point indicates continuity at that point. (See the article derivative’s section on continuity and differentiability.)
•f’s differentiability can be relaxed to one-sided differentiability, as shown in the semi-differentiability article.
Theorem 2: If f’ (x) = g’ (x) for all x in an interval (a, b) of these functions’ domain, then f – g is constant, i.e. f = g + c, where c is a constant on the domain of these functions (a, b).
Proof: If F = f g, then F’ = f’ g’ = 0 on the interval (a, b), implying that F = f g is a constant c or f = g + c according to the previous theorem 1.
Theorem 3: If F is an antiderivative of f on an interval I, then F(x) + c, where c is a constant, is the greatest generic antiderivative of f on I.
Proof: It follows immediately from the second theorem.
Conclusion
The conclusion of the mean value theorem is that if a function f is continuous on the interval [a,b] and differentiable on the interval (a,b), then there exists a point “c” in the interval (a,b) where f′(c) equals the ratio of the difference of the functions f(a) and f(b).