The Mean Value Theorem is a fundamental concept in calculus. The oldest variation of the mean value theorem was established in the 14th century by Parmeshwara, a mathematician from Kerala, India. Furthermore, in the 17th century, Rolle provided a simplified version of this: Rolle’s Theorem, which was only established for polynomials and was not part of the calculus. Augustin Louis Cauchy proposed the present version of the Mean Value Theorem in 1823.
The mean value theorem states that there is one point on a curve that connects two points where the tangent is parallel to the secant that connects the two sites. This mean value theorem is the foundation of Rolle’s theorem.
Definition
The mean value theorem asserts that there is at least one point (c, f(c)) on a curve f(x) passing through two provided points (a, f(a)), (b, f(b)) where the tangent is parallel to the secant travelling through the two given locations. For a function f(x): [a, b] R that is continuous and differentiable across an interval, the mean value theorem is defined in calculus.
•Over the interval [a, b], the function f(x) is continuous.
• function f(x) can be differentiated over a range of values (a, b).
•In (a, b), there is a point c where f’(c) = [f(b) – f(a)] / (b – a)
The tangent at c is parallel to the secant travelling through the points (a, f(a)), (b, f(b) in this proof. This mean value theorem is used to prove a statement across a narrow range. Rolle’s theorem is also used to derive the mean value theorem.
Proof of Mean Value Theorem
Statement: The mean value theorem states that if a function f is continuous over the closed interval [a,b] and differentiable over the open interval (a,b), there must be at least one point c in the interval (a,b) where f(c) is the function’s average rate of change over [a,b] and parallel to the secant line over [a,b].
Proof: Let g(x) be the secant line connecting (a, f(a)) and (b, f(b)) to f(x). We know that the secant line’s equation is y-y1 = m (x- x1).
g(x) – f(a) = [ f(b) – f(a) ] / (b – a) (x-a)
g(x) = [ f(b) – f(a) ] / (b – a) (x-a) + f(a) —🡪(1)
Let h(x) be f(x) – g(x)
h(x) = f(x) – [[ f(b) – f(a) ] / (b – a) (x-a) + f(a)] (From (1))
h(a) = h(b) = 0, and h(x) is differentiable on [a,b] and continuous on [a,b] (a,b).
Using Rolle’s theorem, there must be some x = c in (a,b) for h’(c) to equal 0.
h’(x) = f’(x) – [ f(b) – f(a) ] / (b – a)
For some c in (a,b), h’(c) = 0. Thus
h’(c) = f’(c) – [ f(b) – f(a) ] / (b – a) = 0
f’(c) = [ f(b) – f(a) ] / (b – a)
As a result, the mean value theorem is established.
Note that if the function is not differentiable, even at a single point in the interval, the result may not hold.
Graphical Representation of Mean Value Theorem
The average price When the function f(x) is represented visually, the theorem is easy to understand. We’ll look at two different points (a, f(a)), and (b, f(b)). The secant of the curve is the line linking these locations, which is parallel to the tangent cutting the curve at (c, f(c)). The secant of the curve connecting these locations has the same slope as the tangent at point (c, f(c)). We know that the slope at that point is the tangent’s derivative.
Slope of the Tangent = Secant’s Slope
f’(c) = [ f(b) – f(a) ] / (b – a) 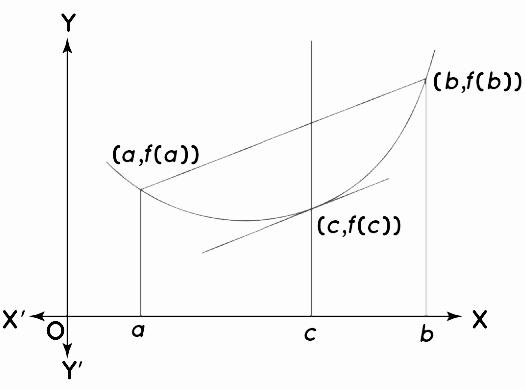
Graph of mean value theorem
The point (c, f(c)) is located between the two points (a, f(a)) and (b, f(b)).
The Mean Value Theorem For Derivatives
If f(x) is continuous on [a,b] and differentiable on (a,b), the Mean Value Theorem asserts that there exists a number c between a and b such that
f’(c) = [ f(b) – f(a) ] / (b – a)
To approximate the values of c that satisfy the conclusion of the Mean Value Theorem, use the applet below. Simply enter the numbers a, b, and c for the function f(x). The applet shows the secant line through the points (a,f(a)) and (b,f(b)), the line parallel to the secant line at the point (c,f(c)), and the line tangent to f(x) at x=c.
Drag the red dot along the curve to change the value of c. When you think you’ve identified a value of c that meets the mean value theorem’s conclusion, click the “Locate” button in the applet’s lower left corner. The applet will change your c value to one that is more accurate and meets the mean value theorem. The tangent line has now become parallel to the secant line.
Application of Mean Value Theorem
The relationship between a function’s derivative and its increasing or decreasing nature is known as the mean value theorem. It essentially describes a differential and continuous function’s derivative. A few key results from the mean value theorem are listed below.
-
Assume the function f is continuous in the interval [a,b] and differentiable on the interval (a,b).
If f’(x) = 0, x (a,b), then f(x) in [a,b] is constant.
-
Define f and g as functions that are continuous in the interval [a,b] and differentiable on the interval [a,b] (a,b),
If f’(x) = g’(x) and x = (a,b), then f(x) – g(x) in [a,b] is constant.
-
Increasing Function Consistently Let f be a function that is continuous in the interval [a, b] and differentiable in the interval [a, b] (a,b)
If f’(x) > 0, x (a,b), then f(x) in [a,b] is a strictly growing function.
-
The Function Is Strictly Decreasing Let f be a function that is continuous in the interval [a,b] and differentiable in the interval [a,b] (a, b)
If f’(x) = 0, x (a,b), then f(x) in [a,b] is a strictly decreasing function.
Conclusion
There exists a point “c” in the interval (a, b) if a function “f” is continuous on the interval [a, b] and also differentiable on the interval (a, b).
F’(c) = [ f(b) – f(a) ] / (b – a)
(i.e.) A point c ∈(a, b) exists where the tangent is parallel to the line passing through the points (a, f(a)) and (b, f(b)).