
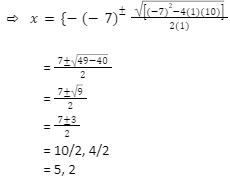
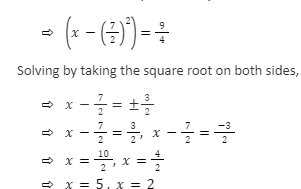
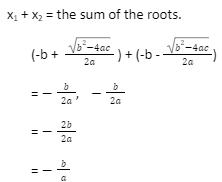
Practical uses of quadratic equations can be traced all the way back to 2050 BC, according to history. Geometric methods were employed by mathematicians in Babylonia, Egypt, Greece, China, and India to solve quadratic equations. Various historians continued to develop new formulas for solving quadratic problems over time.
A Jewish mathematician named Abraham bar Hiyya Ha-Nasi wrote the first European book that featured a comprehensive solution to the general quadratic equation in the 12th century, and René Descartes published La Géométrie in 1637, which contained all of the quadratic equation formula that we know today.
The roots of the quadratic equation ax2 + bx + c = 0 are just the quadratic equation’s solutions. They are, in other words, the values of the variable (x) that satisfy the equation. The x-coordinates of the function’s x-intercepts are the roots of a quadratic function. A quadratic equation can only have two roots because its degree is two. Different methods can be used to locate the roots of quadratic equations.
Factoring
Quadratic Formula
Completing the Square
Graphing
Let us learn about the roots of quadratic equations, including discriminant, nature of the roots, sum of roots, product of roots, and other concepts, as well as some instances.
Quadratic Equation Roots
The roots of quadratic equations are the values of the variables that satisfy the equation. They’re also known as the quadratic equation’s “solutions” or “zeroes.” The roots of quadratic equation, for example.
x2-7x+10=0 are x = 2 and x = 5 because they solve the problem i.e.,
When, x = 2
(2)2- 7(2) + 10 = 4 + 14 + 10 = 28
When, x = 5
(5)2 -7(5) + 10 = 25 – 35 + 10 = 0
But how do you determine the roots of an ax2 + bx + c = 0 quadratic equation? Let’s see if we can solve it for x by filling in the square.
ax2+bx=-c
Now, by dividing both sides with ‘a’, we get

This is the quadratic formula, and it may be used to find any sort of quadratic equation root.
How to Find the Quadratic Equation’s Roots?
“Solving quadratic equations” refers to the process of locating the roots of quadratic equations. The roots of quadratic equation could be obtained using the quadratic formula, as we saw in the previous section. There are various more ways for finding the roots of a quadratic equation in addition to this one.
Let’s look at each of these strategies individually by solving an illustration of finding the roots of the quadratic equation x2 – 7x + 10 = 0. The equation should be in the standard form ax2 + bx + c = 0 in each of these ways.
Factoring to get the roots of a quadratic equation
Consider the left side.
x-2x-5=0
Solve by setting each of these factors to zero.
(x – 2) = 0, (x – 5) = 0
x = 2, x = 5
Finding Roots of a Quadratic Equation Using the Quadratic Formula:
Compare the preceding equation to ax2 + bx + c = 0 to find a, b, and c values.
Then a = 1, b = -7, and c = 10 are the values.
Simplify by substituting them in the quadratic formula.
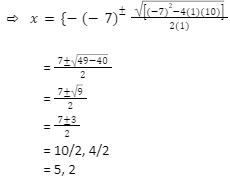
Therefore, x = 2, x = 5
Completing Squares to Find Quadratic Equation Roots
On the left side, complete the square.
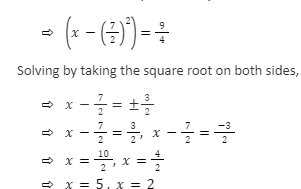
Sum and Product of Quadratic Equation Roots
The roots of the quadratic equation x2 – 7x + 10 = 0 have been found to be x = 2 and x = 5. As a result, the product of its roots = 2 x 5 = 10 and the total of its roots = 2 + 5 = 7. However, without actually computing the roots, the sum and product of roots of a quadratic equation ax2 + bx + c = 0 can be obtained.
The roots of quadratic equation ax2 + bx + c = 0 are (-b + (b2 – 4ac))/2a and (-b – (b2 – 4ac))/2a, according to the quadratic formula. Let us call these x1 and x2, respectively.
Sum of Quadratic Equation Roots
x1 + x2 = the sum of the roots.
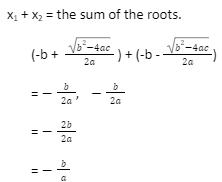
As a result, the roots of the quadratic equation ax2 + bx + c = 0 add up to -b/a.
The sum of the roots for the equation x2 – 7x + 10 = 0 is -(-7)/1 = 7. (Which is the sum of the actual roots 2 & 5).
Conclusion:
Quadratic equations are two-dimensional algebraic expressions. They are classified as higher-order equations. The solution or root of a quadratic equation is the value of a variable for which the equation is fulfilled. The degree of a polynomial equation is equal to the number of roots. A quadratic equation thus has two roots. Let and be the generalised roots of the quadratic equation: ax2 + bx + c = 0. (-b-b2-4ac)/2a and (-b+b2-4ac)/2a are the formulas for solving quadratic equations, respectively.
A, B, & C are all true and sensible. As a result, the nature of the roots and of the equation ax2 + bx + c = 0 is determined by the quantity (b2 – 4ac) under the square root sign. We say this because no real number can be the root of a negative number.
We say this because no real number can be the root of a negative number. A quadratic equation is x2 = -1. As a result, there are no real-number solutions to this problem.