If there does not exist any common elements between two sets then they are said to be disjoint sets. In other words, if the intersection of two sets is empty i.e. no common elements then they are said to be disjoint sets. Disjoint sets are used to solve a variety of arithmetic issues and have applications in data structures.
Definition of disjoint set :-
If the intersection of two sets is a null or empty set, they are said to be disjoint sets. The condition of disjointness holds for a collection of two or more sets if the intersection of the entire collection is an empty set.
Disjoint sets have no common items since the intersection set operation between them always returns a null or empty set. Let’s look at two other sets, X = ( a, b ) and Y = ( c, d ). It is clear that there are no common items between these two groups.
X ∩ Y = phi in this way we can the intersection of these two sets X and Y.
As a result, we can claim that intersection on disconnected sets produces a null set.
The venn diagram representation of the disjoint :-
The relationship between the provided sets can be depicted using a Venn diagram. Venn diagrams can be used to depict the majority of the set operations. Venn diagrams can also be used to illustrate disjoint sets. There is no overlapping region between the disjoint sets on the Venn diagram.
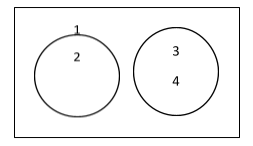
Consider the following two sets: X = ( 1 , 2 ) and Y = ( 3 , 4 ) . The Venn diagram for these two groups is as follows:
We can consider the two given sets, X and Y, as disjoint sets because
they do not have any intersecting or shared elements, and so the
Venn diagram between two disjoint sets will not contain
any overlapping region.
To find if two sets are disjoint :-
We must conduct the intersection of sets operation on two sets in order to determine if they are disjoint sets. The condition that every given set is disjoint can be written as A∩ B = phi.
-
If we have more than two sets, then we can use intersections between all those pairs of sets to see if they are disjoint or not.
-
Once the intersection of that set is complete then we must analyse the results of each pair of the sets, and if any of these pairs of sets result in an empty set, they are deemed disconnected sets.
Pairwise disjoint set :-
A family of collections of subsets is referred to as pairwise disjoint. Let A be the set of a group of sets, with P and Q being two of the sets in A. P and Q are then known as pairwise disjoint sets if and only if they are subsets of A, P is not equal to Q, and P ∩ Q = phi . Mutually disjoint sets are another name for them.
If we take a set of sets, then any pair of sets in that group that intersects with a null intersection can be regarded as pairwise disjoint sets. When the intersection of two sets yields a null set, they are considered pairwise disjoint sets. There are no elements in common between these sets. As a result, pairwise disjoint sets can be compared to disjoint sets.
Points to remember about disjoint sets :-
Here’s a rundown of some key aspects to keep in mind when studying disjoint sets.
-
Disjoint sets have no common items since the intersection set operation between them always returns a null or empty set.
-
When the intersection of two sets results in a null set, they are considered pairwise disjoint sets.
CONCLUSION :-
The sets that intersect with each other and produce a null set are known as disjoint sets. In set theory, we may find that two sets have no common items, in which case the intersection of the sets is called an empty set or null set. A disjoint set is the name for this type of set.
If the intersection of two sets is a null or empty set, they are considered disconnected sets. If the intersection of a collection of two or more sets is an empty set, the condition of disjointness holds. Disjoint sets are used to solve a variety of arithmetic issues and have applications in data structures. If we take a set of sets, then any pair of sets in that group that intersects with a null intersection can be regarded as pairwise disjoint sets.